Question

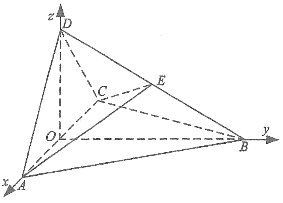
【題目】（2017高考新課標Ⅲ，理19）如圖，四面體ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．

（1）證明：平面ACD⊥平面ABC；

（2）過AC的平面交BD于點E，若平面AEC把四面體ABCD分成體積相等的兩部分，求二面角D–AE–C的余弦值.

Answer 1

【答案】（1）見解析；（2）.

【解析】試題分析：（1）利用題意證得二面角的平面角為90°，則可得到面面垂直；

（2）利用題意求得兩個半平面的法向量，然后利用二面角的夾角公式可求得二面角D–AE–C的余弦值為.

試題解析：（1）由題設可得，，從而.

又是直角三角形，所以.

取AC的中點O，連接DO,BO,則DO⊥AC,DO=AO.

又由于是正三角形，故.

所以為二面角的平面角.

在中，.

又，所以，

故.

所以平面ACD⊥平面ABC.

（2）由題設及（1）知，兩兩垂直，以為坐標原點，的方向為軸正方向，為單位長，建立如圖所示的空間直角坐標系.則.

由題設知，四面體ABCE的體積為四面體ABCD的體積的，從而E到平面ABC的距離為D到平面ABC的距離的，即E為DB的中點，得.

故.

設是平面DAE的法向量，則即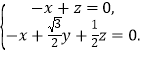

可取.

設是平面AEC的法向量，則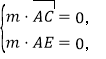同理可取.

則.

所以二面角D-AE-C的余弦值為.