
【題目】已知函數![]() ,
,![]() .
.
(1)證明:![]() 在區間
在區間![]() 上單調遞增;
上單調遞增;
(2)若存在![]() ,使得
,使得![]() 與
與![]() 在
在![]() 的值域相同,求實數
的值域相同,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)求出![]() ,可證明
,可證明![]() ,
,![]() 恒成立,故可得
恒成立,故可得![]() 為
為![]() 上的增函數.
上的增函數.
(2)先討論![]() 時的情形,此時可把
時的情形,此時可把![]() 的存在性問題轉化為
的存在性問題轉化為![]() 在
在![]() 存在兩個不同的零點問題,利用導數和零點存在定理可得
存在兩個不同的零點問題,利用導數和零點存在定理可得![]() .再討論
.再討論![]() 的情形,利用兩個函數的函數值的符號可判定這種情況不成立,兩者結合可求
的情形,利用兩個函數的函數值的符號可判定這種情況不成立,兩者結合可求![]() 的取值范圍.
的取值范圍.
(1)因為![]() ,故
,故![]() 且
且![]() ,
,
令![]() ,故
,故![]() .
.
當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 上為增函數,
上為增函數,
所以![]() ,
,
故![]() ,
,![]() ,故
,故![]() 為
為![]() 上的增函數.
上的增函數.
(2)因為![]() ,故
,故![]() 在
在![]() 為增函數,
為增函數,
故![]() 在
在![]() 上的值域為
上的值域為![]() .
.
當![]() 時,
時,![]() 的值域為
的值域為![]() ,故
,故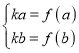 ,
,
所以![]() 在
在![]() 有兩個不同的解
有兩個不同的解![]() .
.
令![]() ,
,
故![]() 在
在![]() 有兩個不同的零點.
有兩個不同的零點.
又![]() ,
,
當![]() 時,
時,![]() ,
,
故![]() 為
為![]() 上的單調增函數,
上的單調增函數,
故![]() 在
在![]() 最多有一個解,舍去.
最多有一個解,舍去.
當![]() 時,
時,![]() .
.
取![]() ,
,![]() ,
,
令![]() ,則
,則![]() ,
,
故![]() 在
在![]() 為增函數,
為增函數,
故![]() ,
,
故![]() 在
在![]() 有且只有一個實數解
有且只有一個實數解![]() 且
且![]() .
.
當![]() ,
,![]() ,故
,故![]() 在
在![]() 為減函數;
為減函數;
當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 為增函數;
為增函數;
故![]() .
.
又![]() ,所以
,所以![]()
因為![]() 在
在![]() 有兩個不同的零點,
有兩個不同的零點,
故![]() 即
即![]() .
.
令![]() ,其中
,其中![]() ,
,
故![]() ,故
,故![]() 在
在![]() 上為減函數,
上為減函數,
故不等式![]() 的解為
的解為![]() ,
,
所以![]() .
.
令![]() 及
及![]() ,
,
因為![]() 為開口向上的二次函數,
為開口向上的二次函數,
故存在![]() ,使得當任意
,使得當任意![]() 時,總有
時,總有![]() ,
,
而![]() ,故
,故![]() 在
在![]() 上為增函數,
上為增函數,
當對任意的![]() 時,總有
時,總有![]() ,
,
因為![]() ,故當
,故當![]() ,
,![]() ,
,
根據零點存在定理,![]() 在
在![]() 上有且只有一個零點.
上有且只有一個零點.
因為![]() 在
在![]() 有兩個不同的零點,故
有兩個不同的零點,故![]() ,
,
所以![]() 即
即![]() ,
,
又![]() ,故
,故![]() ,
,
所以![]() .
.
當![]() 時,
時,![]() 在
在![]() 上始終滿足
上始終滿足![]() ,
,
由(1)可知![]() 在
在![]() 為增函數,故
為增函數,故![]() ,
,
不符合題設要求,舍去.
綜上,![]() .
.


科目:高中數學 來源: 題型:
【題目】南宋數學家楊輝在《詳解九章算法》和《算法通變本末》中,提出了一些新的垛積公式,所討論的高階等差數列與一般等差數列不同,前后兩項之差并不相等,但是逐項差數之差或者高次差成等差數列對這類高階等差數列的研究,在楊輝之后一般稱為“垛積術”.現有高階等差數列,其前7項分別為1,4,8,14,23,36,54,則該數列的第19項為( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,點
中,點![]() 在拋物線
在拋物線![]() :
: ![]() 上,直線
上,直線![]() :
: ![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
, ![]() 兩點,且直線
兩點,且直線![]() ,
, ![]() 的斜率之和為-1.
的斜率之和為-1.
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,設直線
,設直線![]() 與
與![]() 軸交于
軸交于![]() 點,延長
點,延長![]() 與拋物線
與拋物線![]() 交于點
交于點![]() ,拋物線
,拋物線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,記直線
,記直線![]() ,
, ![]() 與
與![]() 軸圍成的三角形面積為
軸圍成的三角形面積為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司收取快遞費用的標準是:重量不超過![]() 的包裹收費10元;重量超過
的包裹收費10元;重量超過![]() 的包裹,除收費10元之外,超過
的包裹,除收費10元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
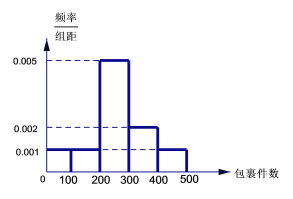
(1)求這60天每天包裹數量的平均值和中位數;
(2)該公司從收取的每件快遞的費用中抽取5元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.已知公司前臺有工作人員3人,每人每天工資100元,以樣本估計總體,試估計該公司每天的利潤有多少元?
(3)小明打算將![]() 四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過
四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過![]() ,求他支付的快遞費為45元的概率.
,求他支付的快遞費為45元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是
的大小是![]() .連接
.連接![]() ,
,![]() ,如圖:
,如圖:
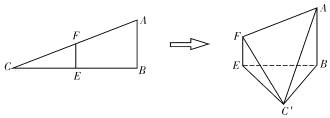
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() .若
.若![]() 為線段
為線段![]() 的中點,則在
的中點,則在![]() 翻折過程中,有下列三個命題:
翻折過程中,有下列三個命題:
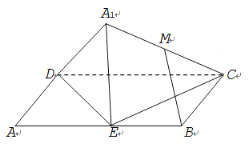
①線段![]() 的長是定值;
的長是定值;
②存在某個位置,使![]() ;
;
③存在某個位置,使![]() 平面
平面![]() .
.
其中正確的命題有______. (填寫所有正確命題的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對![]() 四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”; 乙說:“
作品獲得一等獎”; 乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() 兩件作品未獲得一等獎”; 丁說:“是
兩件作品未獲得一等獎”; 丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
評獎揭曉后,發現這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某小區2017年1月至2018年1月當月在售二手房均價(單位:萬元/平方米)的散點圖.(圖中月份代碼1—13分別對應2017年1月—2018年1月)
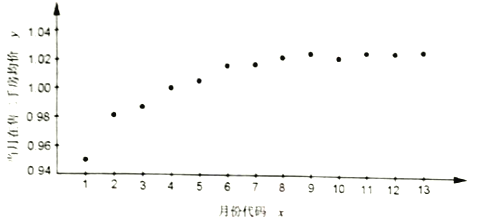
由散點圖選擇![]() 和
和![]() 兩個模型進行擬合,經過數據處理得到兩個回歸方程分別為
兩個模型進行擬合,經過數據處理得到兩個回歸方程分別為![]() 和
和![]() ,并得到以下一些統計量的值:
,并得到以下一些統計量的值:
|
| |
殘差平方和 | 0.000591 | 0.000164 |
總偏差平方和 | 0.006050 | |
(1)請利用相關指數![]() 判斷哪個模型的擬合效果更好;
判斷哪個模型的擬合效果更好;
(2)某位購房者擬于2018年6月份購買這個小區![]() 平方米的二手房(欲
平方米的二手房(欲
購房為其家庭首套房).若購房時該小區所有住房的房產證均已滿2年但未滿5年,請你利用(1)中擬合效果更好的模型估算該購房者應支付的購房金額.(購房金額=房款+稅費;房屋均價精確到0.001萬元/平方米)
附注:根據有關規定,二手房交易需要繳納若干項稅費,稅費是按房屋的計稅價格進行征收.(計稅價格=房款),征收方式見下表:
契稅 (買方繳納) | 首套面積90平方米以內(含90平方米)為1%;首套面積90平方米以上且144平方米以內(含144平方米)為1.5%;面積144平方米以上或非首套為3% |
增值稅 (賣方繳納) | 房產證未滿2年或滿2年且面積在144平方米以上(不含144平方米)為5.6%;其他情況免征 |
個人所得稅 (賣方繳納) | 首套面積144平方米以內(含144平方米)為1%;面積144平方米以上或非首套均為1.5%;房產證滿5年且是家庭唯一住房的免征 |
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 參考公式:相關指數
. 參考公式:相關指數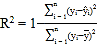 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com