
【題目】已知函數(shù)![]() .
.
(1)若![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若函數(shù)![]() 有兩個不同的零點
有兩個不同的零點![]() ,
,![]() ,且
,且![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】
(1)![]() 恒成立,等價于
恒成立,等價于![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,令
,令![]() ,注意
,注意![]() ,對
,對![]() 分類討論求出
分類討論求出![]() 單調(diào)性即可求解;
單調(diào)性即可求解;
(2)求![]() ,得到
,得到![]() 的單調(diào)區(qū)間,進而求出兩零點的范圍是
的單調(diào)區(qū)間,進而求出兩零點的范圍是![]() ,利用(1)的結(jié)論
,利用(1)的結(jié)論![]() ,
,![]() ,可得
,可得![]() ,再由
,再由![]() 在
在![]() 減函數(shù),可得
減函數(shù),可得![]() ,得到
,得到![]() ,建立
,建立![]() 不等量關(guān)系,即可證明結(jié)論.
不等量關(guān)系,即可證明結(jié)論.
(1)由題意可得![]() 的定義域為
的定義域為![]() ,
,
![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
當![]() 時,即
時,即![]() ;當
;當![]() 時,即
時,即![]() ,
,
構(gòu)造函數(shù)![]() ,
,
 ,
,
令![]() ,可知
,可知![]() 在
在![]() 單調(diào)遞減,在
單調(diào)遞減,在![]() 單調(diào)遞增,
單調(diào)遞增,
當![]() 時,
時,![]() ,則
,則![]() 單調(diào)遞增,故滿足題意,
單調(diào)遞增,故滿足題意,
當![]() 時,
時, ,
,
方程![]() 有兩個不相等的正根
有兩個不相等的正根![]() ,
,![]() ,
,
由于![]() ,所以
,所以![]() ,因此
,因此![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
在![]() 單調(diào)遞減,
單調(diào)遞減,![]() 單調(diào)遞增,
單調(diào)遞增,
因此![]() ,
,![]() ,不滿足題意,
,不滿足題意,
綜上:![]() .
.
(2)由(1)可得![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
所以![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減,
單調(diào)遞減,
所以![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
所以在![]() 和
和![]() 各存在一個零點,由題設(shè)可知
各存在一個零點,由題設(shè)可知![]() ,
,
因此![]() ,則
,則![]() …①,
…①,
因為![]() 在
在![]() 單調(diào)遞減,因此
單調(diào)遞減,因此![]() ,
,
即 ,
,
所以![]() …②,
…②,
由①②可得:![]() ,
,
化簡可得![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】“割圓術(shù)”是劉徽最突出的數(shù)學成就之一,他在《九章算術(shù)注》中提出割圓術(shù),并作為計算圓的周長,面積已經(jīng)圓周率的基礎(chǔ),劉徽把圓內(nèi)接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數(shù)值,這個結(jié)果是當時世界上圓周率計算的最精確數(shù)據(jù).如圖,當分割到圓內(nèi)接正六邊形時,某同學利用計算機隨機模擬法向圓內(nèi)隨機投擲點,計算得出該點落在正六邊形內(nèi)的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數(shù)據(jù):![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知平行四邊形![]() 中
中![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,三角形
,三角形![]() 為等邊三角形,
為等邊三角形,![]() ,
,![]() .
.![]() ,
,![]() 分別為線段
分別為線段![]() ,
,![]() 的中點.
的中點.
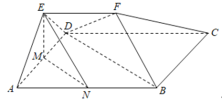
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為F.
的右焦點為F.
(1)求點F的坐標和橢圓C的離心率;
(2)直線![]() 過點F,且與橢圓C交于P,Q兩點,如果點P關(guān)于x軸的對稱點為
過點F,且與橢圓C交于P,Q兩點,如果點P關(guān)于x軸的對稱點為![]() ,判斷直線
,判斷直線![]() 是否經(jīng)過x軸上的定點,如果經(jīng)過,求出該定點坐標;如果不經(jīng)過,說明理由.
是否經(jīng)過x軸上的定點,如果經(jīng)過,求出該定點坐標;如果不經(jīng)過,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】各項均為非負整數(shù)的數(shù)列{an}同時滿足下列條件:
①a1=m(m![]() N*);②ann-1(n≥2);③n是a1+a2+‥+an的因數(shù)(n ≥1).
N*);②ann-1(n≥2);③n是a1+a2+‥+an的因數(shù)(n ≥1).
(Ⅰ)當m=5時,寫出數(shù)列{an}的前五項;
(Ⅱ)若數(shù)列{an}的前三項互不相等,且n≥3時,an為常數(shù),求m的值;
(Ⅲ)求證:對任意正整數(shù)m,存在正整數(shù)M,使得n≥M時,an為常數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】 已知函數(shù)f(x)=|x+a|+|x-2|.
(1)當a=-3時,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,
,![]() 為橢圓上異于長軸端點的點,且
為橢圓上異于長軸端點的點,且![]() 的最大面積為
的最大面積為![]() .
.
(1)求橢圓![]() 的標準方程
的標準方程
(2)若直線![]() 是過點
是過點![]() 點的直線,且
點的直線,且![]() 與橢圓
與橢圓![]() 交于不同的點
交于不同的點![]() 、
、![]() ,是否存在直線
,是否存在直線![]() 使得點
使得點![]() 、
、![]() 到直線
到直線![]() ,的距離
,的距離![]() 、
、![]() ,滿足
,滿足![]() 恒成立,若存在,求
恒成立,若存在,求![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】動圓![]() 過定點
過定點![]() ,且在
,且在![]() 軸上截得的弦
軸上截得的弦![]() 的長為4.
的長為4.
(1)若動圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(2)在曲線![]() 的對稱軸上是否存在點
的對稱軸上是否存在點![]() ,使過點
,使過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 的交點
的交點![]() 滿足
滿足![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標及定值;若不存在,請說明理由.
的坐標及定值;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com