
定義在R上的單調函數f(x)滿足f(3)=log23且對任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求證f(x)為奇函數;
(2)若f(k·3 )+f(3
)+f(3 -9
-9 -2)<0對任意x∈R恒成立,求實數k的取值范圍.
-2)<0對任意x∈R恒成立,求實數k的取值范圍.
(1)見解析
(2)  R恒成立.
R恒成立.
【解析】(1)證明奇偶性根據定義,可根據x,y取值的任意性,給x,y賦值,顯然可以令y=-x,所以需要令x=y=0,求出f(0)的值.問題基本就可以解決.
(2)本小題可根據奇函數這個條件把不等式轉化為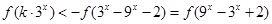 ,然后再研究函數f(x)的單調性,利用單調性把不等式中函數值的大小關系轉化為變量的大小關系,從而脫掉法則符號f,求解即可
,然后再研究函數f(x)的單調性,利用單調性把不等式中函數值的大小關系轉化為變量的大小關系,從而脫掉法則符號f,求解即可
(1)證明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,則有
0=f(x)+f(-x).即f(-x)=-f(x)對任意x∈R成立,所以f(x)是奇函數.
(2)解:f(3)=log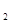 3>0,即f(3)>f(0),又f(x)在R上是單調函數,所以f(x)在R上是增函數,又由(1)f(x)是奇函數.
3>0,即f(3)>f(0),又f(x)在R上是單調函數,所以f(x)在R上是增函數,又由(1)f(x)是奇函數.
f(k·3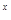 )<-f(3
)<-f(3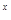 -9
-9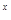 -2)=f(-3
-2)=f(-3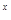 +9
+9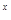 +2), k·3
+2), k·3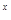 <-3
<-3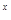 +9
+9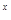 +2,
+2,
3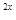 -(1+k)·3
-(1+k)·3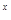 +2>0對任意x∈R成立.
+2>0對任意x∈R成立.
令t=3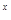 >0,問題等價于t
>0,問題等價于t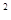 -(1+k)t+2>0對任意t>0恒成立.
-(1+k)t+2>0對任意t>0恒成立.




 R恒成立
R恒成立


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2-x | x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| f(-2-an) |
| 1 |
| 2 |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 4 |
| 3 |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| a2n |
| 12 |
| 35 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| f(n) |
| 1 |
| 2n |
| 4 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com