【題目】同時具有性質：“①最小正周期是π；②圖象關于直線 
對稱；③在 
上是增函數．”的一個函數為（ ）
A.
B.
??
C.
D.
【答案】D
【解析】解：由于y=sin（ 
+ 
）的最小正周期為 
=4π，不滿足①，故排除A． 由于y=cos（ ﹣ ）的最小正周期為 =4π，不滿足①，故排除B．
由于y=cos（2x+ ），在 
上，2x+ ∈[﹣ ， 
]，
故y=cos（2x+ ）在 上沒有單調性，故排除C．
對于y=sin（2x﹣ ）的最小正周期為 
=π；
當 
時，函數取得最大值為1，故圖象關于直線 對稱；
在 上，2x﹣ ∈[﹣ 
， ]，故y=sin（2x﹣ ）在 上是增函數，
故D滿足題中的三個條件，
故選：D．
【考點精析】根據題目的已知條件，利用正弦函數的單調性和正弦函數的對稱性的相關知識可以得到問題的答案，需要掌握正弦函數的單調性：在
上是增函數；在
上是減函數；正弦函數的對稱性：對稱中心
；對稱軸
．
科目：高中數學 來源： 題型：
【題目】為了監控某種零件的一條生產線的生產過程，檢驗員每天從該生產線上隨機抽取16個零件，并測量其尺寸（單位： 
）．根據長期生產經驗，可以認為這條生產線正常狀態下生產的零件的尺寸服從正態分布
．
（1）假設生產狀態正常，記
表示一天內抽取的16個零件中其尺寸在
之外的零件數，求
及
的數學期望；
（2）一天內抽檢零件中，如果出現了尺寸在
之外的零件，就認為這條生產線在這一天的生產過程可能出現了異常情況，需對當天的生產過程進行檢查．
（ⅰ）試說明上述監控生產過程方法的合理性；
（ⅱ）下面是檢驗員在一天內抽取的16個零件的尺寸：
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
經計算得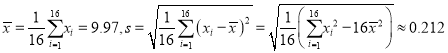
，其中
為
抽取的第
個零件的尺寸， 
．
用樣本平均數
作為
的估計值
，用樣本標準差
作為
的估計值
，利用估計值判斷是否需對當天的生產過程進行檢查？剔除
之外的數據，用剩下的數據估計
和
（精確到0.01）．
附：若隨機變量
服從正態分布
，則
， 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,在直三棱柱ABCA1B1C1中,D是BC的中點．
(1)求證:A1B∥平面ADC1;
(2)若AB⊥AC,AB＝AC＝1,AA1＝2,求幾何體ABD-A1B1C1的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
（
）的左焦點為
，左準線方程為
.
（1）求橢圓
的標準方程；
（2）已知直線
交橢圓
于
， 
兩點.
①若直線
經過橢圓
的左焦點
，交
軸于點
，且滿足
， 
.求證： 
為定值；
②若
（
為原點），求
面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若方程
所表示的曲線為C，給出下列四個命題：
①若C為橢圓，則
；
②若C為雙曲線，則
或
；
③曲線C不可能是圓；
④若
，曲線C為橢圓，且焦點坐標為
；
⑤若，曲線C為雙曲線，且虛半軸長為
．
其中真命題的序號為____________.（把所有正確命題的序號都填在橫線上）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一輛賽車在一個周長為
的封閉跑道上行駛，跑道由幾段直道和彎道組成，圖
反映了賽車在“計時賽”整個第二圈的行駛速度與行駛路程之間的關系．
圖1
圖2
根據圖有以下四個說法：
①在這第二圈的
到
之間，賽車速度逐漸增加；
②在整個跑道中，最長的直線路程不超過
；
③大約在這第二圈的
到之間，賽車開始了那段最長直線路程的行駛；
④在圖
的四條曲線（注：
為初始記錄數據位置）中，曲線
最能符合賽車的運動軌跡．
其中，所有正確說法的序號是（ ）
A. ①②③ B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-5：不等式選講]已知函數f（x）=|2x﹣a|+a．
（1）當a=2時，求不等式f（x）≤6的解集；
（2）設函數g（x）=|2x﹣1|，當x∈R時，f（x）+g（x）≥3，求a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
