
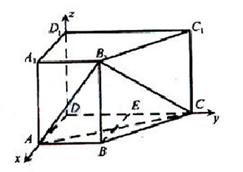
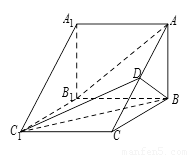
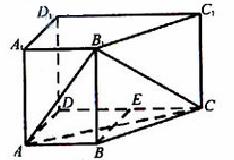
如圖,在四棱柱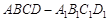 中,側棱
中,側棱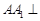 底面
底面 ,
,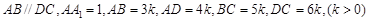
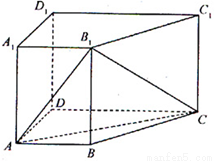
(Ⅰ)求證: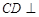 平面
平面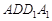
(Ⅱ)若直線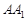 與平面
與平面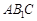 所成角的正弦值為
所成角的正弦值為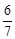 ,求
,求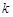 的值
的值
(Ⅲ)現(xiàn)將與四棱柱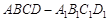 形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規(guī)定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為
形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規(guī)定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為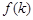 ,寫出
,寫出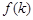 的解析式。(直接寫出答案,不必說明理由)
的解析式。(直接寫出答案,不必說明理由)
(Ⅰ)見解析(Ⅱ)1(Ⅲ)共有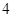 種不同的方案
種不同的方案

【解析】(Ⅰ)取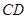 中點
中點 ,連接
,連接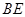
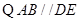 ,
,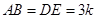
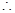 四邊形
四邊形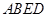 為平行四邊形
為平行四邊形
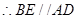 且
且
在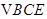 中,
中,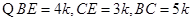
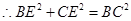
 ,即
,即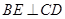 ,又
,又 ,所以
,所以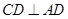
 平面
平面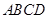 ,
,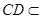 平面
平面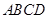
 ,又
,又 ,
,
 平面
平面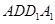
(Ⅱ)以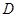 為原點,
為原點,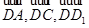 的方向為
的方向為 軸的正方向建立如圖所示的空間直角坐標系
軸的正方向建立如圖所示的空間直角坐標系 ,
, ,
,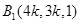 ,
,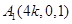
所以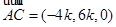 ,
,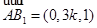 ,
,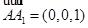
設平面 的法向量
的法向量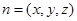 ,則由
,則由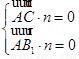
得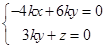 取
取 ,得
,得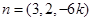
設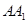 與平面
與平面 所成角為
所成角為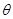 ,則
,則
 ,解得
,解得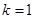 .故所求
.故所求 的值為1
的值為1
(Ⅲ)共有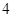 種不同的方案
種不同的方案
立體幾何第一問對于關系的決斷往往基于對公理定理推論掌握的比較熟練,又要善于做出一線輔助線加以證明,那么第二問就可以在其基礎上采用坐標法處理角度或者距離問題,坐標法所用的公式就必需熟練掌握,第三問主要考查了學生的空間思維能力,要在平時多加練習。此題坐標法也很考驗學生的計算功底。
【考點定位】 本題主要考查立體幾何中線線關系線面關系的判斷以及線面角的算法,并且通過第三問的設問又把幾何體的表面積與函數(shù)巧妙的結合起來,計算和空間思維要求比較高。屬于難題。


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數(shù)學 來源:2013-2014學年四川成都石室中學高三模擬考試一文科數(shù)學試卷(解析版) 題型:解答題
如圖,在三棱柱 中,側棱
中,側棱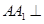 底面
底面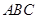 ,
,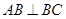 ,
, 為
為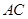 的中點,
的中點,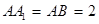 .
.
(Ⅰ)求證: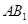 //平面
//平面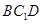 ;
;
(Ⅱ)設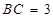 ,求四棱錐
,求四棱錐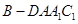 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源:2014屆廣東省高一下學期期中考試數(shù)學試卷(解析版) 題型:解答題
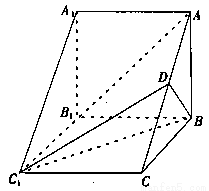
如圖,在三棱柱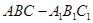 中,側棱
中,側棱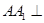 底面
底面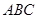 ,
,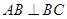 ,
,
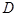 為
為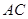 的中點,
的中點,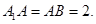
(1)求證: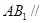 平面
平面 ;
;
(2)過點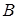 作
作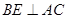 于點
于點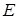 ,求證:直線
,求證:直線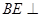 平面
平面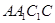
(3)若四棱錐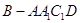 的體積為3,求
的體積為3,求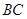 的長度
的長度
查看答案和解析>>
科目:高中數(shù)學 來源:2011年山東省濟寧市高二上學期期中考試文科數(shù)學 題型:選擇題
如圖,在四棱柱 中,底面
中,底面 是正方形,側棱與底面垂直,
是正方形,側棱與底面垂直, 分別是
分別是 ,
, 的中點,則以下結論中不成立的是( )
的中點,則以下結論中不成立的是( )

A. 與
與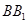 垂直
B.
垂直
B. 與
與 垂直
垂直
C. 與
與 異面
D.
異面
D. 與
與 異面
異面
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
如圖,在四棱柱![]() 中,側棱
中,側棱![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
(1)求證:![]()
(2)若直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的值;
的值;
(3)現(xiàn)將與四棱柱![]() 形狀和大小完全相同的兩個四棱柱拼接成一個新的棱柱,規(guī)定:若拼接成的新的四棱柱形狀和大小完全相同,則視為同一種拼接方案.問:共有幾種不同的方案?在這些拼接成的新四棱柱中,記其中最小的表面積為
形狀和大小完全相同的兩個四棱柱拼接成一個新的棱柱,規(guī)定:若拼接成的新的四棱柱形狀和大小完全相同,則視為同一種拼接方案.問:共有幾種不同的方案?在這些拼接成的新四棱柱中,記其中最小的表面積為![]() ,寫出
,寫出![]() 的表達式(直接寫出答案,不必要說明理由)
的表達式(直接寫出答案,不必要說明理由)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com