Question

【題目】設，函數(shù)．

（1）當時，求函數(shù)的單調區(qū)間；

（2）若函數(shù)在區(qū)間上有唯一零點，試求a的值．

Answer 1

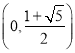【答案】（1）的單調減區(qū)間是，單調增區(qū)間是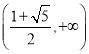；（2）.

【解析】

（1）將代入中可得（）,令,解得,進而求得單調區(qū)間；

（2）令,解得（舍）,,可得函數(shù)在上單調遞減,在上單調遞增,則,由于函數(shù)在區(qū)間上有唯一零點,則,整理即為,設,可得在是單調遞增的,則,進而求得

（1）函數(shù),

當時,（）,

∴,

令,即,

解得或（舍）,

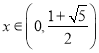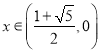∴時,；時,,

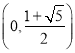∴的單調減區(qū)間是,單調增區(qū)間是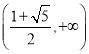

（2）,

則,

令,得,

∵,

∴,

∴方程的解為（舍）,；

∴函數(shù)在上單調遞減,在上單調遞增，

∴,

若函數(shù)在區(qū)間上有唯一零點,

則,

而滿足,

∴,

即,

設,

∵在是單調遞增的,

∴至多只有一個零點,

而,

∴用代入,

得,

解得