
【題目】選修4—1:幾何證明選講
如圖,四邊形![]() 內(nèi)接于⊙
內(nèi)接于⊙![]() ,過點
,過點![]() 作⊙
作⊙![]() 的切線
的切線![]() 交
交![]() 的延長線于
的延長線于![]() ,已知
,已知![]() .
.

證明:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)詳見解析;(2)詳見解析。
【解析】
試題分析:
(1)由題可知,EP為圓O的切線,切點為A,AD為過點A的圓的弦,則∠EAD為弦切角,那么根據(jù)弦切角等于它所夾的弧所對的圓周角可知,∠EAD=∠ACD,又因為已知條件∠EAD=∠PAC,所以得到∠ACD=∠PCA,而∠ACD,∠PCA都為圓周角,圓周角相等,則它們所對的弧相等,所對的弦相等,所以得出AD=AB,問題得證;
(2)欲證![]() 成立,只需證明
成立,只需證明![]() 成立,而根據(jù)第(1)問AD=AB,所以問題轉(zhuǎn)化為證明
成立,而根據(jù)第(1)問AD=AB,所以問題轉(zhuǎn)化為證明![]() ,所以只需證出
,所以只需證出![]() ∽
∽![]() 即可,因為四邊形
即可,因為四邊形![]() 內(nèi)接于⊙
內(nèi)接于⊙![]() ,
,
∴![]() .又
.又![]() ,∴
,∴![]() ∽
∽![]() .于是問題得證。本題考查平面幾何三角形相似,弦切角定理。
.于是問題得證。本題考查平面幾何三角形相似,弦切角定理。
試題解析:(1)∵![]() 與⊙
與⊙![]() 相切于點
相切于點![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵四邊形![]() 內(nèi)接于⊙
內(nèi)接于⊙![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ∽
∽![]() .
.
∴![]() ,即
,即![]() ,
,
∴![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,對一切正整數(shù)
,對一切正整數(shù)![]() ,點
,點![]() 都在函數(shù)
都在函數(shù)![]() 的圖象上,記
的圖象上,記![]() 與
與![]() 的等差中項為
的等差中項為![]() 。
。
(Ⅰ)求數(shù)列![]() 的通項公式;
的通項公式;
(Ⅱ)若![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(Ⅲ)設(shè)集合![]() ,等差數(shù)列
,等差數(shù)列![]() 的任意一項
的任意一項![]() ,其中
,其中![]() 是
是![]() 中的最小數(shù),且
中的最小數(shù),且![]() ,求
,求![]() 的通項公式。
的通項公式。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,且OA·OB=2,其中
兩點,且OA·OB=2,其中![]() 為原點.
為原點.
(1)求拋物線![]() 的方程;
的方程;
(2)點![]() 坐標(biāo)為
坐標(biāo)為![]() ,記直線
,記直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從某大學(xué)一年級女生中,選取身高分別是150cm、155cm、160cm、165cm、170cm的學(xué)生各一名,其身高和體重數(shù)據(jù)如表所示:
身高/cm ( | 150 | 155 | 160 | 165 | 170 |
體重/kg ( | 43 | 46 | 49 | 51 | 56 |
(1)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)利用(1)中的回歸方程,計算身高為168cm時,體重的估計值![]() 為多少?
為多少?
參考公式:線性回歸方程![]() ,其中
,其中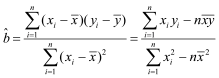 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校高中畢業(yè)班有男生![]() 人,女生
人,女生![]() 人,學(xué)校為了對高三學(xué)生數(shù)學(xué)學(xué)習(xí)情況進(jìn)行分析,從高三年級按照性別進(jìn)行分層抽樣,抽取
人,學(xué)校為了對高三學(xué)生數(shù)學(xué)學(xué)習(xí)情況進(jìn)行分析,從高三年級按照性別進(jìn)行分層抽樣,抽取![]() 名學(xué)生成績,統(tǒng)計數(shù)據(jù)如下表所示:
名學(xué)生成績,統(tǒng)計數(shù)據(jù)如下表所示:
分?jǐn)?shù)段(分) |
|
|
|
|
| 總計 |
頻數(shù) |
|
|
|
|
|
|
(1)若成績在![]() 分以上(含
分以上(含![]() 分),則成績?yōu)榧案?請估計該校畢業(yè)班平均成績和及格學(xué)生人數(shù);
分),則成績?yōu)榧案?請估計該校畢業(yè)班平均成績和及格學(xué)生人數(shù);
(2)如果樣本數(shù)據(jù)中,有60名女生數(shù)學(xué)成績及格,請完成如下數(shù)學(xué)成績與性別的列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為:“該校學(xué)生的數(shù)學(xué)成績與性別有關(guān)”.
的把握認(rèn)為:“該校學(xué)生的數(shù)學(xué)成績與性別有關(guān)”.
女生 | 男生 | 總計 | |
及格人數(shù) |
| ||
不及格人數(shù) | |||
總計 |
參考公式:![]()
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】堯盛機(jī)械生產(chǎn)廠每生產(chǎn)某產(chǎn)品![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為
(萬元),其中固定成本為![]() 萬元,并且每生產(chǎn)1百臺的生產(chǎn)成本為1萬元(總成本=固定成本+生產(chǎn)成本).銷售收入
萬元,并且每生產(chǎn)1百臺的生產(chǎn)成本為1萬元(總成本=固定成本+生產(chǎn)成本).銷售收入![]() (萬元)滿足
(萬元)滿足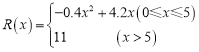 ,假定生產(chǎn)的產(chǎn)品都能賣掉,請完成下列問題:
,假定生產(chǎn)的產(chǎn)品都能賣掉,請完成下列問題:
(1)寫出利潤函數(shù)![]() 的解析式(注:利潤=銷售收入-總成本);
的解析式(注:利潤=銷售收入-總成本);
(2)試問該工廠生產(chǎn)多少臺產(chǎn)品時,可使盈利最多?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)如圖,在平面直角坐標(biāo)系![]() 中, 已知
中, 已知![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點
的左、右焦點![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點,
的左、右頂點,![]() 為線段
為線段![]() 的中點, 且
的中點, 且![]() .
.
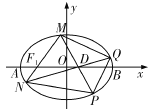
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓
為橢圓![]() 上的動點(異于點
上的動點(異于點![]() ),連接
),連接![]() 并延長交橢圓
并延長交橢圓![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() 并分別延
并分別延
長交橢圓![]() 于點
于點![]() 連接
連接![]() ,設(shè)直線
,設(shè)直線![]() 、
、![]() 的斜率存在且分別為
的斜率存在且分別為![]() 、
、![]() ,試問是否存在常數(shù)
,試問是否存在常數(shù)![]() ,使
,使
得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】命題“若x>0,則x2>0”的否命題是( )
A.若x>0,則x2≤0
B.若x2>0,則x>0
C.若x≤0,則x2≤0
D.若x2≤0,則x≤0
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com