
【題目】已知向量 ![]() ,將函數
,將函數 ![]() 的圖象按向量
的圖象按向量 ![]() 平移后得到函數g(x)的圖象.
平移后得到函數g(x)的圖象.
(1)求函數g(x)的表達式;
(2)若函數 ![]() 上的最小值為h(a),求h(a)的最大值.
上的最小值為h(a),求h(a)的最大值.
【答案】
(1)解:設P(x,y)是函數y=f(x)圖象上的任意一點,它在函數y=g(x)圖象上的對應點P'(x',y'),則由平移公式,得
∴ 代入函數 中,
得
∴函數y=g(x)的表達式為
(2)解:函數g(x)的對稱軸為
①當 即 時,函數g(x)在[ ]上為增函數,
∴ ;
②當 即 時,
∴
當且僅當 時取等號;
③當 即 時,函數g(x)在[ ]上為減函數,
∴
綜上可知,
∴當 時,函數h(a)的最大值為
【解析】(1)利用圖象平移的知識,根據向量平移的公式建立平移之后的圖象上點的坐標與平移之前圖象上點的坐標之間的關系是解決本題的關鍵;(2)利用(1)中得到的函數關系式,確定該函數是二次函數類型,根據對稱軸與函數定義區間的關系,結合分類討論思想求出函數的最小值的表達式是解決本題的關鍵.
【考點精析】通過靈活運用函數的最值及其幾何意義,掌握利用二次函數的性質(配方法)求函數的最大(小)值;利用圖象求函數的最大(小)值;利用函數單調性的判斷函數的最大(小)值即可以解答此題.


科目:高中數學 來源: 題型:
【題目】已知全集為實數集R,集合A={x|y= ![]() +
+ ![]() },B={x|log2x>1}.
},B={x|log2x>1}.
(1)分別求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求實數a的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我校要從參加數學競賽的1000名學生中,隨機抽取50名學生的成績進行分析,現將參加數學競賽的1000名學生編號如下000,001,002,…,999,如果在第一組隨機抽取的一個號碼為015,則抽取的第40個號碼為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解高三年級學生寒假期間的學習情況,某學校抽取了甲、乙兩班作為對象,調查這兩個班的學生在寒假期間平均每天學習的時間(單位:小時),統計結果繪成頻率分布直方圖(如圖).已知甲、乙兩班學生人數相同,甲班學生平均每天學習時間在區間![]() 的有8人.
的有8人.
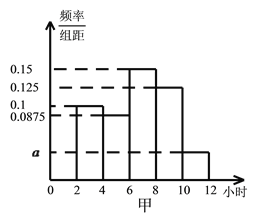

(I)求直方圖中![]() 的值及甲班學生平均每天學習時間在區間
的值及甲班學生平均每天學習時間在區間![]() 的人數;
的人數;
(II)從甲、乙兩個班平均每天學習時間大于10個小時的學生中任取4人參加測試,設4人中甲班學生的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com