
【題目】已知函數![]() ,
,
(Ⅰ)若![]() ,求
,求![]() 的單調區間;(Ⅱ)若
的單調區間;(Ⅱ)若![]() 有最大值3,求
有最大值3,求![]() 的值;(Ⅲ)若
的值;(Ⅲ)若![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范圍。
的取值范圍。
【答案】(Ⅰ)![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增. (Ⅱ)
單調遞增. (Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
試題分析:(Ⅰ)將原函數分解為兩個基本初等函數,借助于復合函數單調性判定方法可求得函數單調區間;(Ⅱ)由函數有最大值可知原函數先增后減,所以二次函數先減后增,及二次函數取得最小值-1,由此可得a的值;(Ⅲ)由函數值域可得![]() 可取的所有得正數,結合二次函數性質可求得
可取的所有得正數,結合二次函數性質可求得![]() 的取值范圍
的取值范圍
試題解析:(Ⅰ)當![]() 時,
時,![]() ,令
,令![]() ,由于
,由于![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 單調遞減,而
單調遞減,而![]() 在
在![]() 上單調遞減,
上單調遞減,![]()
![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增. …………4分
單調遞增. …………4分
(Ⅱ)令![]() ,
,![]() ,由于
,由于![]() 有最大值3,所以
有最大值3,所以![]() 應有最小值-1,因此
應有最小值-1,因此![]() ,解得
,解得![]() .…………8分
.…………8分
(Ⅲ)由指數函數的性質可知,要使![]() 的值域為
的值域為![]() ,則
,則![]() 的值域應為
的值域應為![]() ,因此只能是
,因此只能是![]() ,因為若
,因為若![]() ,則
,則![]() 為二次函數,值域不可能是
為二次函數,值域不可能是![]() ,故
,故![]() 的取值范圍是
的取值范圍是![]() .…12分
.…12分


科目:高中數學 來源: 題型:
【題目】某市出租車的計價標準是4 km以內10元(含4 km),超過4 km且不超過18 km的部分1.5元/km,超出18 km的部分2元/km.
(1)如果不計等待時間的費用,建立車費y元與行車里程x km的函數關系式;
(2)如果某人乘車行駛了30 km,他要付多少車費?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l1經過兩點(-1,-2),(-1,4),直線l2經過兩點(2,1),(6,y),且l1⊥l2,則y=( )
A. -2 B. 1 C. 2 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個命題與它的逆命題,否命題,逆否命題這四個命題中( )
A. 假命題與真命題的個數相同
B. 真命題的個數是奇數
C. 真命題的個數是偶數
D. 假命題的個數是奇數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD﹣A1B1C1D1的棱長為1,線段B1D1上有兩個動點E,F,且EF=![]() ,則下列結論中錯誤的是( )
,則下列結論中錯誤的是( )
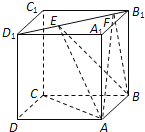
A.AC⊥BE
B.EF∥平面ABCD
C.三棱錐A﹣BEF的體積為定值
D.異面直線AE,BF所成的角為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個年級有12個班,每個班有50名同學,隨機編號為1~50,為了了解他們在課外的興趣,要求每班第40號同學留下來進行問卷調查,這里運用的抽樣方法是( )
A. 抽簽法 B. 分層抽樣法
C. 隨機數表法 D. 系統抽樣法
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,過其焦點
,過其焦點![]() 作兩條相互垂直且不平行于坐標軸的直線,它們分別交拋物線
作兩條相互垂直且不平行于坐標軸的直線,它們分別交拋物線![]() 于點
于點![]() 、
、![]() 和點
和點![]() 、
、![]() ,線段
,線段![]() 、
、![]() 的中點分別為
的中點分別為![]() 、
、![]() .
.
(Ⅰ)求線段![]() 的中點
的中點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)求![]() 面積的最小值;
面積的最小值;
(Ⅲ)過![]() 、
、![]() 的直線
的直線![]() 是否過定點?若是,求出定點坐標,若不是,請說明理由.
是否過定點?若是,求出定點坐標,若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com