【答案】
分析:(1)討論含參數的函數的單調性問題,先求出導函數f′(x),令f′(x)>0,本小題要對參數a分a≥0,-1<a<0,a≤-1三種情形進行討論,對運算能力要求較高;
(2),由(1)的結論-1<a=
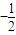
<0,所以分三個單調區間來利用單調性來討論函數的零點的個數問題.
(3)是近年來高考考查的熱點問題,即與函數結合證明不等式問題,常用的解題思路是利用前面的結論構造函數,利用函數的單調性,對于函數取單調區間上的正整數自變量n有某些結論成立,進而解答出這類不等式問題的解.
解答:解:(1)
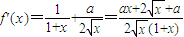
,
若a≥0,則f′(x)>0,f(x)在定義域內單調遞增;若a≤-1,
則f′(x)<0,f(x)在定義域內單調遞減;若-1<a<0,由f′(x)=0
解得,
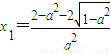
,
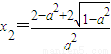
,
直接討論f′(x)知,f(x)在
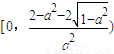
和
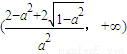
單調遞減,
在
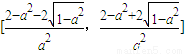
單調遞增.
(2)觀察得f(0)=0,
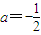
時,
由①得f(x)在
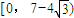
單調遞減,
所以f(x)在
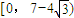
上有且只有一個零點;
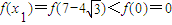
,
計算得
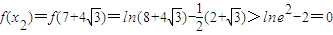
,
f(x
1)f(x
2)<0且f(x)在區間
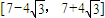
單調遞增,
所以f(x)在
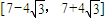
上有且只有一個零點;
根據對數函數與冪函數單調性比較知,
存在充分大的M∈R,使f(M)<0,f(x
2)f(M)<0
且f(x)在區
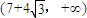
單調遞減,
所以f(x)在
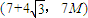
上
從而在
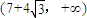
上有且只有一個零點.
綜上所述,
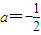
時,f(x)有3個零點.
(3)取a=-1,
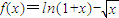
,
由①得f(x)單調遞減,
所以?x>0,f(x)<f(0)=0,
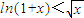
,
從而ln(1+
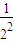
)(1+
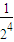
)…(1+
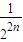
)
=ln(1+
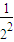
)ln(1+
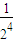
)+…(1+
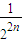
)
<

+

+…
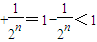
,
由lnx單調遞增得
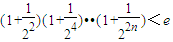
.
點評:單調性刻畫函數兩個變量變化趨勢的一致性,是認識函數的重要角度,運用單調性可以確定函數零點的個數,考查導數使單調性可以定量、精確研究這一重要工具.參數是可變的常數,處理參數是比較高端的數學素養,本題考查了這一素養,因此對學生的綜合應用能力要求較高.

 ,a∈R是常數.
,a∈R是常數.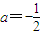 時,f(x)零點的個數;
時,f(x)零點的個數;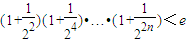 (n∈N*,e為自然對數的底數).
(n∈N*,e為自然對數的底數).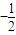 <0,所以分三個單調區間來利用單調性來討論函數的零點的個數問題.
<0,所以分三個單調區間來利用單調性來討論函數的零點的個數問題.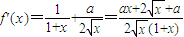 ,
,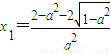 ,
,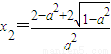 ,
,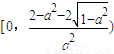
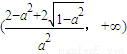 單調遞減,
單調遞減,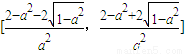 單調遞增.
單調遞增.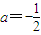 時,
時,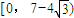 單調遞減,
單調遞減,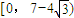 上有且只有一個零點;
上有且只有一個零點;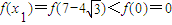 ,
,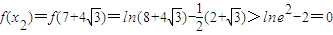 ,
,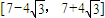 單調遞增,
單調遞增,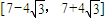 上有且只有一個零點;
上有且只有一個零點;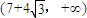 單調遞減,
單調遞減,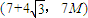 上
上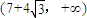 上有且只有一個零點.
上有且只有一個零點.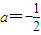 時,f(x)有3個零點.
時,f(x)有3個零點.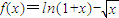 ,
,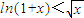 ,
,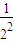 )(1+
)(1+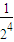 )…(1+
)…(1+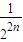 )
)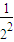 )ln(1+
)ln(1+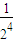 )+…(1+
)+…(1+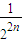 )
) +
+ +…
+…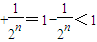 ,
,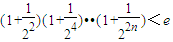 .
.
