【題目】已知
是函數
的極值點.
（Ⅰ）求實數
的值；
（Ⅱ）求證：函數
存在唯一的極小值點
，且
.
（參考數據：
，
，其中
為自然對數的底數）
【答案】(Ⅰ) 
(Ⅱ)見證明
【解析】
(Ⅰ)根據
，求得實數
的值，通過導數驗證函數單調，可知時極值點為
，滿足題意；
(Ⅱ)由(Ⅰ) 函數
的極小點值位于
，此時
的零點位于
，且此
為的極小點值點，代入，中，化簡即可得到關于的二次函數，求解二次函數在區(qū)間
上的值域即可證明結論。
解：(Ⅰ)因為
，且 是極值點，
所以
，所以 .
此時
，設
，則
.
則當
時，
為減函數.
又
，
所以在
時，
， 為增函數；
時，
，為減函數.所以為的極大值點，符合題意.
（Ⅱ）當
時，
，為增函數，且
，
所以存在
當
時， ，為減函數；
時， ， 為增函數，所以函數存在唯一的極小值點 .
又
，已知
，可得
，
所以
，所以
，
且滿足
.
所以
.
其中
也可以用如下方式證明：
，設
，
則
.
則當
時，
，
為減函數；當
時，
， 為增函數.
所以
所以在
，所以
科目：高中數學 來源： 題型：
【題目】某校命制了一套調查問卷（試卷滿分均為100分），并對整個學校的學生進行了測試，先從這些學生的成績中隨機抽取了50名學生的成績，按照
分成5組，制成了如圖所示的頻率分布直方圖（假定每名學生的成績均不低于50分）
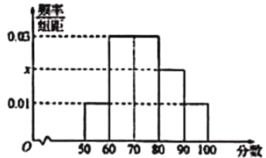
（1）求頻率分布直方圖中的
的值，并估計50名學生的成績的平均數、中位數（同一組中的數據用該組區(qū)間的中點值代表）
（2）用樣本估計總體，若該校共有2000名學生，試估計該校這次成績不低于70分的人數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是橢圓
：
的左焦點，O為坐標原點，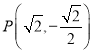
為橢圓上的點．
（1）求橢圓的標準方程；
（2）若點
都在橢圓上，且
中點
在線段
（不包括端點）上，求
面積的最大值，及此時直線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC的三邊BC，CA，AB的中點分別是D(5，3)，E(4，2)，F(1，1).
（1）求△ABC的邊AB所在直線的方程及點A的坐標；
（2）求△ABC的外接圓的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC的三邊BC，CA，AB的中點分別是D(5，3)，E(4，2)，F(1，1).
（1）求△ABC的邊AB所在直線的方程及點A的坐標；
（2）求△ABC的外接圓的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某大型超市公司計劃在
市新城區(qū)開設分店，為確定在新城區(qū)開設分店的個數，該公司對該市已開設分店的其他區(qū)的數據統(tǒng)計后得到下列信息（其中
表示在該區(qū)開設分店的個數，
表示這個分店的年收入之和）：
分店個數 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
（Ⅰ）該公司經過初步判斷，可用線性回歸模型擬合與的關系，求關于的回歸方程；
（Ⅱ）假設該公司每年在新城區(qū)獲得的總利潤
（單位：萬元）與，之間的關系為
，請根據（Ⅰ）中的線性回歸方程，估算該公司在新城區(qū)開設多少個分店時，才能使新城區(qū)每年每個分店的平均利潤最大.
參考公式：回歸方程
中斜率和截距的最小二乘估計公式分別為：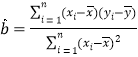
，
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
