
【題目】已知函數f(x)=lnx﹣mx(m∈R).
(1)若曲線y=f(x)過點P(1,﹣1),求曲線y=f(x)在點P的切線方程;
(2)若f(x)≤0恒成立求m的取值范圍;
(3)求函數f(x)在區間[1,e]上最大值.
【答案】
(1)解:∵f(x)過點P(1,﹣1),
∴﹣1=ln1﹣m,∴m=1,
∴f(x)=lnx﹣x,
![]() ,
,
f'(1)=0,
∴過點P(1,﹣1)的切線方程為y=﹣1
(2)解:∵f(x)≤0恒成立,
即lnx﹣mx≤0恒成立,
∴mx≥lnx,
又∵f(x)定義域為(0,+∞),
∴ ![]() 恒成立;
恒成立;
設 ![]() ,
,
∵ ![]() ,
,
∴當x=e時,g'(e)=0
當0<x<e時,g'(x)>0,g(x)為單調增函數,
當x>e時,g'(x)<0,g(x)為單調減函數,
∴ ![]() ,
,
∴當 ![]() 時,f(x)≤0恒成立
時,f(x)≤0恒成立
(3)解:∵ ![]() ,
,
①當m≤0時,f'(x)>0,
∴f(x)在(0,+∞)為單增函數,
∵在x∈[1,e]上,f(x)max=f(e)=1﹣me;
②當 ![]() ,即
,即 ![]() 時,
時,
當 ![]() 時,f'(x)>0,f(x)為單增函數,
時,f'(x)>0,f(x)為單增函數,
當 ![]() 時,f'(x)<0,f(x)為單減函數,
時,f'(x)<0,f(x)為單減函數,
∴x∈[1,e]上, ![]() ;
;
③當m>1時,即 ![]() 在
在 ![]() 為單減函數,
為單減函數,
∴x∈[1,e]上,f(x)max=f(1)=﹣m;
④當 ![]() ,即
,即 ![]() 時,
時,
f(x)在 ![]() 為單增函數,
為單增函數,
∴x∈[1,e]時,f(x)max=f(e)=1﹣me;
綜上所述,
當 ![]() 時,f(x)max=f(e)=1﹣me,
時,f(x)max=f(e)=1﹣me,
當 ![]() 時,
時, ![]()
當m>1時,f(x)max=f(1)=﹣m
【解析】(1)由f(x)過點P(1,﹣1)可得﹣1=ln1﹣m,從而解出m=1,進而求曲線y=f(x)在點P的切線方程;(2)原式可化為lnx﹣mx≤0恒成立,結合x>0可化為 ![]() 恒成立,從而化為求
恒成立,從而化為求 ![]() 的最大值,利用導數求最值;(3)由
的最大值,利用導數求最值;(3)由 ![]() 討論,m的取值,以確定函數函數f(x)在區間[1,e]上的單調性,從而求函數在區間[1,e]上的最大值.
討論,m的取值,以確定函數函數f(x)在區間[1,e]上的單調性,從而求函數在區間[1,e]上的最大值.
【考點精析】利用函數的最大(小)值與導數對題目進行判斷即可得到答案,需要熟知求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數學 來源: 題型:
【題目】在等比數列{an}中,a1=1,且a2是a1與a3﹣1的等差中項.
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足 ![]() .求數列{bn}的前n項和
.求數列{bn}的前n項和 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 是[1,∞]上的增函數.當實數m取最大值時,若存在點Q,使得過Q的直線與曲線y=g(x)圍成兩個封閉圖形,且這兩個封閉圖形的面積總相等,則點Q的坐標為( )
是[1,∞]上的增函數.當實數m取最大值時,若存在點Q,使得過Q的直線與曲線y=g(x)圍成兩個封閉圖形,且這兩個封閉圖形的面積總相等,則點Q的坐標為( )
A.(0,﹣3)
B.(0,3)
C.(0,﹣2)
D.(0,2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,為保護河上古橋OA,規劃建一座新橋BC,同時設立一個圓形保護區.規劃要求:新橋BC與河岸AB垂直;保護區的邊界為圓心M在線段OA上并與BC相切的圓,且古橋兩端O和A到該圓上任意一點的距離均不少于80 m.經測量,點A位于點O正北方向60 m處,點C位于點O正東方向170 m處(OC為河岸),tan∠BCO=![]() .
.
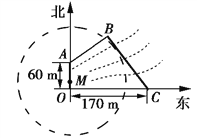
(1)求新橋BC的長;
(2)當OM多長時,圓形保護區的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x
(1)試求函數F(x)=f(x)+f(2x),x∈(﹣∞,0]的最大值;
(2)若存在x∈(﹣∞,0),使|af(x)﹣f(2x)|>1成立,試求a的取值范圍;
(3)當a>0,且x∈[0,15]時,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題中:
①某地市高三理科學生有15000名,在一次調研測試中,數學成績 ![]() 服從正態分布
服從正態分布 ![]() ,已知
,已知 ![]() ,若按成績分層抽樣的方式抽取100份試卷進行分析,則應從120分以上(包括120分)的試卷中抽取
,若按成績分層抽樣的方式抽取100份試卷進行分析,則應從120分以上(包括120分)的試卷中抽取 ![]() 份;
份;
②已知命題 ![]() ,則
,則 ![]() :
: ![]() ;
;
③在 ![]() 上隨機取一個數
上隨機取一個數 ![]() ,能使函數
,能使函數 ![]() 在
在 ![]() 上有零點的概率為
上有零點的概率為 ![]() ;
;
④設 ![]() ,則“
,則“ ![]() ”是“
”是“ ![]() ”的充要條件.
”的充要條件.
其中真命題的序號為.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x-a)(x-b)(其中a>b),若f(x)的圖象如圖所示,則函數g(x)=ax+b的圖象大致為( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是雙曲線
是雙曲線![]() 上一點,
上一點, ![]() ,
, ![]() 分別是雙曲線左、右兩個焦點,若
分別是雙曲線左、右兩個焦點,若![]() ,則
,則![]() 等于( )
等于( )
A. 1 B. 17 C. 1或17 D. 以上答案均不對
【答案】B
【解析】根據雙曲線的定義得到![]() 根據雙曲線的焦半徑的范圍得到
根據雙曲線的焦半徑的范圍得到![]() 故結果為17.
故結果為17.
故答案為:B。
【題型】單選題
【結束】
10
【題目】某中學學生會為了調查愛好游泳運動與性別是否有關,通過隨機詢問110名性別不同的高中生是否愛好游泳運動得到如下的列聯表:由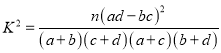 并參照附表,得到的正確結論是( )
并參照附表,得到的正確結論是( )
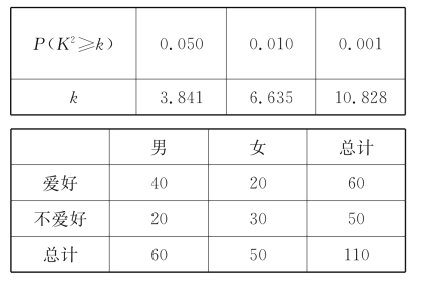
A. 在犯錯誤的概率不超過![]() 的前提下,認為“愛好游泳運動與性別有關”
的前提下,認為“愛好游泳運動與性別有關”
B. 在犯錯誤的概率不超過![]() 的前提下,認為“愛好游泳運動與性別無關”
的前提下,認為“愛好游泳運動與性別無關”
C. 有![]() 的把握認為“愛好游泳運動與性別有關”
的把握認為“愛好游泳運動與性別有關”
D. 有![]() 的把握認為“愛好游泳運動與性別無關”
的把握認為“愛好游泳運動與性別無關”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com