
(本小題滿分7分)選修4-4:坐標系與參數(shù)方程
已知曲線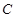 的極坐標方程是
的極坐標方程是 .以極點為平面直角坐標系的原點,極軸為
.以極點為平面直角坐標系的原點,極軸為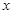 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線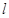 的參數(shù)方程是
的參數(shù)方程是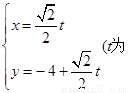 參數(shù)),點
參數(shù)),點 是曲線
是曲線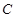 上的動點,點
上的動點,點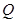 是直線
是直線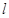 上的動點,求|
上的動點,求|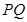 |的最小值.
|的最小值.
解:(Ⅰ)因為橢圓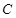 的一個焦點是(1,0),所以半焦距
的一個焦點是(1,0),所以半焦距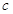 =1.因為橢圓兩個焦點與短軸的一個端點構(gòu)成等邊三角形.
=1.因為橢圓兩個焦點與短軸的一個端點構(gòu)成等邊三角形.
所以 ,解得
,解得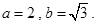
所以橢圓的標準方程為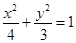 . …4分
. …4分
(Ⅱ)(i)設(shè)直線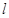 :
: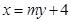 與
與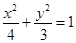 聯(lián)立并消去
聯(lián)立并消去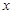 得:
得: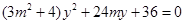 .記
.記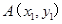 ,
,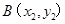 ,
,
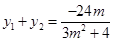 ,
,
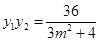 . ……………5分
. ……………5分
由A關(guān)于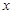 軸的對稱點為
軸的對稱點為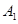 ,得
,得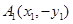 ,
,
根據(jù)題設(shè)條件設(shè)定點為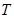 (
(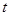 ,0),
,0),
得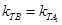 ,即
,即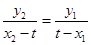 .
.
所以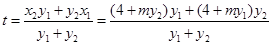
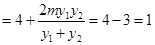
即定點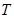 (1 , 0).
……………………………8分
(1 , 0).
……………………………8分
(ii)由(i)中判別式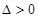 ,解得
,解得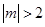 . 可知直線
. 可知直線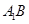 過定點
過定點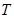 (1,0).
(1,0).
所以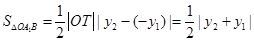 ………10分
………10分
得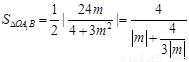 , 令
, 令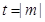
記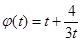 ,得
,得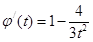 ,當
,當 時,
時,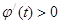 .
.
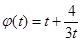 在
在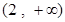 上為增函數(shù). 所以
上為增函數(shù). 所以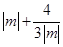
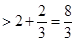 ,
,
得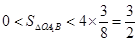 .故△OA1B的面積取值范圍是
.故△OA1B的面積取值范圍是 . ……………13分
. ……………13分
【解析】略


 舉一反三單元同步過關(guān)卷系列答案
舉一反三單元同步過關(guān)卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
|
| x2 |
| 4 |
|
| π |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 5 |
| π |
| 4 |
| a |
| b |
| c |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011屆福建省高考模擬試題(1) 題型:解答題
(1)(本小題滿分7分) 選修4一2:矩陣與變換
若點A(2,2)在矩陣 對應(yīng)變換的作用下得到的點為B(-2,2),求矩陣M的逆矩陣.
對應(yīng)變換的作用下得到的點為B(-2,2),求矩陣M的逆矩陣.
(2)(本小題滿分7分) 選修4一4:坐標系與參數(shù)方程
已知極坐標系的極點O與直角坐標系的原點重合,極軸與x軸的正半軸重合,曲線C1: 與曲線C2:
與曲線C2: (t∈R)交于A、B兩點.求證:OA⊥OB.
(t∈R)交于A、B兩點.求證:OA⊥OB.
(3)(本小題滿分7分) 選修4一5:不等式選講
求證: ,
, .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年福建省泉州市高三畢業(yè)班質(zhì)量檢查理科數(shù)學(xué)試卷(解析版) 題型:解答題
本題有(1)、(2)、(3)三個選答題,每小題7分,請考生任選2個小題作答,滿分14分.如果多做,則按所做的前兩題記分.作答時,先用2B鉛筆在答題卡上把所選題目對應(yīng)的題號涂黑,并將所選題號填入括號中.
(1)(本小題滿分7分)選修4—2:矩陣與變換
在平面直角坐標系 中,把矩陣
中,把矩陣 確定的壓縮變換
確定的壓縮變換 與矩陣
與矩陣 確定的旋轉(zhuǎn)變換
確定的旋轉(zhuǎn)變換 進行復(fù)合,得到復(fù)合變換
進行復(fù)合,得到復(fù)合變換 .
.
(Ⅰ)求復(fù)合變換 的坐標變換公式;
的坐標變換公式;
(Ⅱ)求圓
 在復(fù)合變換
在復(fù)合變換 的作用下所得曲線
的作用下所得曲線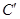 的方程.
的方程.
(2)(本小題滿分7分)選修4-4:坐標系與參數(shù)方程
在平面直角坐標系 中,直線
中,直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),
為參數(shù)), 、
、 分別為直線
分別為直線 與
與 軸、
軸、 軸的交點,線段
軸的交點,線段 的中點為
的中點為 .
.
(Ⅰ)求直線 的直角坐標方程;
的直角坐標方程;
(Ⅱ)以坐標原點 為極點,
為極點, 軸的正半軸為極軸建立極坐標系,求點
軸的正半軸為極軸建立極坐標系,求點 的極坐標和直線
的極坐標和直線 的極坐標方程.
的極坐標方程.
(3)(本小題滿分7分)選修4—5:不等式選講
已知不等式 的解集與關(guān)于
的解集與關(guān)于 的不等式
的不等式 的解集相等.
的解集相等.
(Ⅰ)求實數(shù) ,
, 的值;
的值;
(Ⅱ)求函數(shù)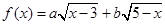 的最大值,以及取得最大值時
的最大值,以及取得最大值時 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年福建省福州市高三第五次質(zhì)量檢查數(shù)學(xué)理卷 題型:解答題
(1)(本小題滿分7分)
選修4-4:矩陣與變換
已知矩陣
 ,A的一個特征值
,A的一個特征值 ,其對應(yīng)的特征向量是
,其對應(yīng)的特征向量是 .
.
(Ⅰ)求矩陣 ;
;
(Ⅱ)求直線 在矩陣M所對應(yīng)的線性變換下的像的方程
在矩陣M所對應(yīng)的線性變換下的像的方程
(2)
(本小題滿分7分)選修4-4:坐標系與參數(shù)方程
已知曲線C的極坐標方程是 .以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線l的參數(shù)方程是:
.以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線l的參數(shù)方程是: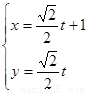 ,求直線l與曲線C相交所成的弦的弦長.
,求直線l與曲線C相交所成的弦的弦長.
((3)(本小題滿分7分)
選修4-5:不等式選講 解不等式∣2x-1∣<∣x∣+1
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com