
【題目】如圖所示,在四棱錐E-ABCD中,平面ABCD⊥平面AEB,且四邊形ABCD為矩形.∠BAE=90°,AE=4,AD=2,F,G,H分別為BE,AE,AD的中點.
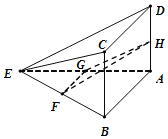
(Ⅰ)求證:CD∥平面FGH;
(Ⅱ)求證:平面FGH⊥平面ADE;
(Ⅲ)在線段DE求一點P,使得AP⊥FH,并求出AP的值.
【答案】(Ⅰ)見解析;(Ⅱ)見解析;(Ⅲ)![]()
【解析】
(Ⅰ)根據三角形中位線性質以及矩形性質得CD∥FG,再根據線面平行判定定理得結論,(Ⅱ)先根據線面垂直判定定理得AB⊥平面ADE,再根據平行得GF⊥平面ADE,最后根據面面垂直判定定理得結論,(Ⅲ)作AP⊥DE于P,再根據線面垂直判定與性質定理得AP⊥FH,再根據面面垂直性質定理得AE⊥平面ABCD,即得AE⊥AD,最后根據直角三角形解得AP的值.
(Ⅰ)證明:在矩形ABCD中,CD∥AB,
∵F,G分別為BE,AE的中點,∴FG∥AB,∴CD∥FG,
∵CD![]() 平面FGH,FG平面FGH,
平面FGH,FG平面FGH,
∴CD∥平面FGH.
(Ⅱ)證明:在矩形ABCD中,AD⊥AB,又∵∠BAE=90°,∴AB⊥AE,又AD∩AE=A
∴AB⊥平面ADE,又GF∥AB∴GF⊥平面ADE,
∵GF平面FGH,∴平面FGH⊥平面ADE.
(Ⅲ)作AP⊥DE于P,∵GF⊥平面ADE,且AP平面ADE,∴GF⊥AP,
∵G,H分別為AE,AD的中點,∴GH∥DE, ∵AP⊥DE∴GH⊥AP
∵GF∩GH=G,∴AP⊥平面FGH,
∵FH平面FGH,∴AP⊥FH,
∵矩形ABCD⊥平面AEB,且平面ABCD∩平面AEB=AB,
∴AE⊥平面ABCD,∴AE⊥AD,
在直角三角形AED中,AE=4,AD=2,可求得![]() .故AP的值為:
.故AP的值為:![]() .
.



 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
【題目】某中學為了組建一支業余足球隊,在高一年級隨機選取50名男生測量身高,發現被測男生的身高全部在160cm到184cm之間,將測量結果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,...,第6組
,...,第6組![]() ,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
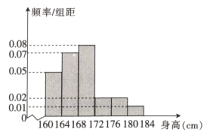
(1)若學校要從中選1名男生擔任足球隊長,求被選取的男生恰好在第5組或第6組的概率;
(2)現在從第5與第6組男生中選取兩名同學擔任守門員,求選取的兩人中最多有1名男生來自第5組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,在區間
,在區間![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,設函數
,設函數![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)方程![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列四個命題:
(1)“若![]() ,則
,則![]() ,
,![]() 互為倒數”的逆命題;
互為倒數”的逆命題;
(2)“面積相等的三角形全等”的否命題;
(3)“若![]() ,則
,則![]() 無實數解”的否命題;
無實數解”的否命題;
(4)命題:“空間中到一個正四面體的六條棱所在的直線距離均相等的點有且只有![]() 個”; 其中真命題( )
個”; 其中真命題( )
A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(1)(2)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過點![]() 作互相垂直的直線
作互相垂直的直線![]() ,
,![]() ,
,![]() 交
交![]() 正半軸于
正半軸于![]() 點,
點,![]() 交
交![]() 正半軸于
正半軸于![]() 點,則線段
點,則線段![]() 中點
中點![]() 軌跡方程為_______________________;過原點
軌跡方程為_______________________;過原點![]() 與
與![]() 、
、![]() 、
、![]() 四點的圓半徑的最小值為______________.
四點的圓半徑的最小值為______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com