
【題目】某鮮花小鎮圈定一塊半徑為1百米的圓形荒地,準備建成各種不同鮮花景觀帶.為了便于游客觀賞,準備修建三條道路AB,BC,CA,其中A,B,C分別為圓上的三個進出口,且A,B分別在圓心O的正東方向與正北方向上,C在圓心O南偏西某一方向上.在道路AC與BC之間修建一條直線型水渠MN種植水生觀賞植物黃鳶尾(其中點M,N分別在BC和CA上,且M在圓心O的正西方向上,N在圓心O的正南方向上),并在區域MNC內種植柳葉馬鞭草.
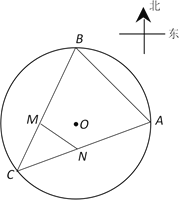
(1)求水渠MN長度的最小值;
(2)求種植柳葉馬鞭草區域MNC面積的最大值(水渠寬度忽略不計).
【答案】(1)![]() 百米;(2)
百米;(2)![]() 平方米.
平方米.
【解析】
(1)設![]() ,
,![]() 可表示出直線
可表示出直線![]() 的方程,從而求得
的方程,從而求得![]() 兩點坐標,進而將
兩點坐標,進而將![]() 表示為關于
表示為關于![]() 的函數,利用導數求得最值;(2)方法一:將
的函數,利用導數求得最值;(2)方法一:將![]() 表示為
表示為![]() ,利用
,利用![]() 將面積表示出來,利用
將面積表示出來,利用![]() 進行換元,從而化簡得:
進行換元,從而化簡得:![]() ,再根據
,再根據![]() 的范圍求得面積最大值;方法二:利用三角形面積公式,直接用
的范圍求得面積最大值;方法二:利用三角形面積公式,直接用![]() 表示出
表示出![]() ,再利用
,再利用![]() 換元,也可得到
換元,也可得到![]() ,從而與方法一采用相同的求最大值方法求值.
,從而與方法一采用相同的求最大值方法求值.
【解】(1)以圓心![]() 為原點,建立平面直角坐標系,則圓
為原點,建立平面直角坐標系,則圓![]() 的方程為
的方程為![]()
設點![]() ,
,![]()
直線![]() 的方程為
的方程為![]() ,令
,令![]() ,得
,得![]()
直線![]() 的方程為
的方程為![]() ,令
,令![]() ,得
,得![]()
所以![]()
令![]() ,
,![]()
即![]() ,
,![]()
則![]()
令![]() ,得
,得![]()
當![]() 時,
時,![]() ,則
,則![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,則
,則![]() 單調遞增;
單調遞增;
所以當![]() 時,
時,![]()
所以![]()
水渠![]() 長度的最小值為
長度的最小值為![]() 百米
百米
(2)由(1)可知,![]() ,
,![]() ,且
,且![]()
則![]()
設![]() ,因為
,因為![]() ,所以
,所以![]()
所以![]() ,
,![]()
所以當![]() 時,
時,![]()
種植柳葉馬鞭草區域![]() 面積的最大值為
面積的最大值為![]() 平方百米
平方百米
另法:(2)因為![]() ,所以
,所以![]()
由![]()
![]()
所以![]()
![]()
設![]() ,因為
,因為![]() ,所以
,所以![]()
所以![]() ,
,![]()
所以當![]() 時,
時,![]()
種植柳葉馬鞭草區域![]() 面積的最大值為
面積的最大值為![]() 平方百米
平方百米


科目:高中數學 來源: 題型:
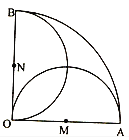
【題目】如圖,在圓心角為直角的扇形OAB區域中,M、N分別為OA、OB的中點,在M、N兩點處各有一個通信基站,其信號的覆蓋范圍分別為以OA、OB為直徑的圓,在扇形OAB內隨機取一點,則此點無信號的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的個數是( )
①相關系數![]() 用來衡量兩個變量之間線性關系的強弱,
用來衡量兩個變量之間線性關系的強弱,![]() 越接近于1,相關性越弱;
越接近于1,相關性越弱;
②回歸直線![]() 過樣本點中心
過樣本點中心![]() ;
;
③相關指數![]() 用來刻畫回歸的效果,
用來刻畫回歸的效果,![]() 越小,說明模型的擬合效果越不好.
越小,說明模型的擬合效果越不好.
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形![]() 的邊長為
的邊長為![]() 米,圓
米,圓![]() 的半徑為
的半徑為![]() 米,圓心是正方形的中心,點
米,圓心是正方形的中心,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,若線段
上,若線段![]() 與圓
與圓![]() 有公共點,則稱點
有公共點,則稱點![]() 在點
在點![]() 的“盲區”中,已知點
的“盲區”中,已知點![]() 以
以![]() 米/秒的速度從
米/秒的速度從![]() 出發向
出發向![]() 移動,同時,點
移動,同時,點![]() 以
以![]() 米/秒的速度從
米/秒的速度從![]() 出發向
出發向![]() 移動,則在點
移動,則在點![]() 從
從![]() 移動到
移動到![]() 的過程中,點
的過程中,點![]() 在點
在點![]() 的盲區中的時長約________秒(精確到
的盲區中的時長約________秒(精確到![]() ).
).
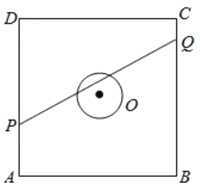
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
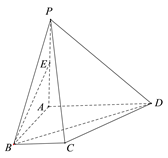
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(i)過點![]() 作一直線
作一直線![]() 與
與![]() 平行,在圖中畫出直線
平行,在圖中畫出直線![]() 并說明理由;
并說明理由;
(ii)求平面![]() 將三棱錐
將三棱錐![]() 分成的兩部分體積的比.
分成的兩部分體積的比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且左焦點F1到左準線的距離為4.
,且左焦點F1到左準線的距離為4.

(1)求橢圓![]() 的方程;
的方程;
(2)若與原點距離為1的直線l1:![]() 與橢圓
與橢圓![]() 相交于A,B兩點,直線l2與l1平行,且與橢圓
相交于A,B兩點,直線l2與l1平行,且與橢圓![]() 相切于點M(O,M位于直線l1的兩側).記△MAB,△OAB的面積分別為S1,S2,若
相切于點M(O,M位于直線l1的兩側).記△MAB,△OAB的面積分別為S1,S2,若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
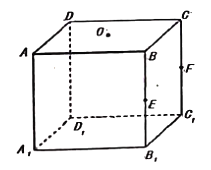
【題目】如下圖,在正方體![]() 中,點
中,點![]() 分別為棱
分別為棱![]() ,
,![]() 的中點,點
的中點,點![]() 為上底面的中心,過
為上底面的中心,過![]() 三點的平面把正方體分為兩部分,其中含
三點的平面把正方體分為兩部分,其中含![]() 的部分為
的部分為![]() ,不含
,不含![]() 的部分為
的部分為![]() ,連接
,連接![]() 和
和![]() 的任一點
的任一點![]() ,設
,設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則![]() 的最大值為( )
的最大值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
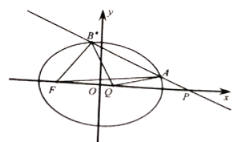
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 短軸的一個頂點到一個焦點的距離等于
短軸的一個頂點到一個焦點的距離等于![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設經過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,點
兩點,點![]() .
.
①若對任意直線![]() 總存在點
總存在點![]() ,使得
,使得![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
②設點![]() 為橢圓
為橢圓![]() 的左焦點,若點
的左焦點,若點![]() 為
為![]() 的外心,求實數
的外心,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
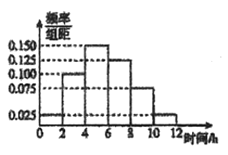
【題目】為調查某校學生每周課外閱讀的情況,采用分層抽樣的方法,收集100位學生每周課外閱讀時間的樣本數據(單位:小時).根據這100個數據,制作出學生每周課外閱讀時間的頻率分布直方圖(如圖).
(1)估計這100名學生每周課外閱讀的平均數![]() 和樣本方差
和樣本方差![]() (同一組數據用該組區間的中點值作代表);
(同一組數據用該組區間的中點值作代表);
(2)由頻率分布直方圖知,該校學生每周課外閱讀時間![]() 近似服從正態分布
近似服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
①求![]() ;
;
②若該校共有10000名學生,記每周課外閱讀時間在區間![]() 的人數為
的人數為![]() ,試求
,試求![]() .
.
參數數據:![]() ,若
,若![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com