某高校設計了一個實驗學科的實驗考查方案：考生從6道備選題中一次性隨機抽取3題，按照題目要求獨立完成全部實驗操作。規定：至少正確完成其中2題的便可提交通過。已知6道備選題中考生甲有4道題能正確完成，2道題不能完成。
（1）求出甲考生正確完成題數的概率分布列，并計算數學期望；
（2）若考生乙每題正確完成的概率都是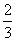
，且每題正確完成與否互不影響。試從至少正確完成2題的概率分析比較兩位考生的實驗操作能力．
智能訓練練測考系列答案
計算高手系列答案科目：高中數學 來源： 題型：解答題
甲、乙、丙三人獨立破譯同一份密碼，已知甲、乙、丙各自破譯出密碼的概率分別為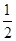
、
、
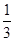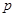，且他們是否破譯出密碼互不影響，若三人中只有甲破譯出密碼的概率為
．
（1）求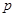的值．
（2）設甲、乙、丙三人中破譯出密碼的人數為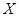
，求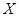的分布列和數學期望
．
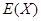查看答案和解析>>
科目：高中數學 來源： 題型：解答題
市民李生居住在甲地,工作在乙地,他的小孩就讀的小學在丙地,三地之間的道路情
況如圖所示.假設工作日不走其它道路,只在圖示的道路中往返,每次在路口選擇道路是隨機
的.同一條道路去程與回程是否堵車相互獨立. 假設李生早上需要先開車送小孩去丙地小學，
再返回經甲地趕去乙地上班.假設道路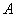
、
、
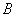上下班時間往返出現擁堵的概率都是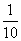
,
道路
、
上下班時間往返出現擁堵的概率都是
，只要遇到擁堵上學和上班的都會遲到.
（1）求李生小孩按時到校的概率；
（2）李生是否有八成把握能夠按時上班？
（3）設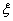
表示李生下班時從單位乙到達小學丙遇到擁堵的次數，求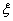的均值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
“H7N9禽流感”問題越來越引起社會關注，我校對高一600名學生進行了一次“H7N9禽流感”知識測試，并從中抽取了部分學生的成績（滿分100分）作為樣本，繪制了下面尚未完成的頻率分布表和頻率分布直方圖．
（1）填寫答題卡頻率分布表中的空格，補全頻率分布直方圖,并標出每個小矩形對應的縱軸數據；
（2）試估計該年段成績在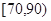
段的有多少人；
（3）請你估算該年級的平均分.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
由于某高中建設了新校區，為了交通方便要用三輛通勤車從老校區把教師接到新校區.已知從新校區到老校區有兩條公路，汽車走一號公路堵車的概率為
，不堵車的概率為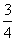
；汽車走二號公路堵車的概率為p，不堵車的概率為1－p，若甲、乙兩輛汽車走一號公路，丙汽車由于其他原因走二號公路，且三輛車是否堵車相互之間沒有影響.
(Ⅰ)若三輛汽車中恰有一輛汽車被堵的概率為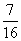
，求走二號公路堵車的概率；
(Ⅱ)在(Ⅰ)的條件下，求三輛汽車中被堵車輛的個數ξ的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
一個袋中裝有大小相同的球10個，其中紅球8個，黑球2個，現從袋中有放回地取球，每次隨機取1個． 求：
（1）連續取兩次都是紅球的概率；
（2）如果取出黑球，則取球終止，否則繼續取球，直到取出黑球，但取球次數最多不超過4次，求取到黑球的概率。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為了防止受到核污染的產品影響我國民眾的身體健康，要求產品進入市場前必須進行兩輪核放射檢測，只有兩輪都合格才能進行銷售。已知某產品第一輪檢測不合格的概率為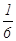
，第二輪檢測不合格的概率為
，兩輪檢測是否合格相互沒有影響。
（1）求該產品不能銷售的概率
（2）如果產品可以銷售，則每件產品可獲利40元；如果產品不能銷售，則每件產品虧損80元（即獲利-80元）。已知一箱中有4件產品，記可銷售的產品數為X，求X的分布列，并求一箱產品獲利的均值。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
兩枚質量均勻的正方體骰子，六個面上分別標有數字1、2、3、4、5、6，拋擲兩枚骰子．記兩枚骰子朝上的面上的數字分別為p，q，若把p，q分別作為點A的橫坐標和縱坐標，
（1）用列表法或樹狀圖表示出點A（p，q）所有可能出現的結果；
（2）求點A（p，q）在函數y=x-1的圖象上的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
； 
，
，所以
，
2分
，則
，所以
，
6分
且
， 8分
的分布列的關鍵是要搞清
，其中：
，記函數
滿足條件：
的事件為A，求事件A發生的概率。