
【題目】已知橢圓![]() :
:![]() 的兩個焦點分別為
的兩個焦點分別為![]() 和
和![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() 和
和![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且滿足
上,且滿足![]() ,當
,當![]() 變化時,給出下列三個命題:
變化時,給出下列三個命題:
①點![]() 的軌跡關于
的軌跡關于![]() 軸對稱;②
軸對稱;②![]() 的最小值為2;
的最小值為2;
③存在![]() 使得橢圓
使得橢圓![]() 上滿足條件的點
上滿足條件的點![]() 僅有兩個,
僅有兩個,
其中,所有正確命題的序號是__________.
 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.
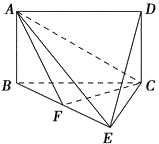
(1)求證:平面AEC⊥平面ABE;
(2)點F在BE上.若DE∥平面ACF,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某中學學生對《中華人民共和國交通安全法》的了解情況,調查部門在該校進行了一次問卷調查(共12道題),從該校學生中隨機抽取40人,統計了每人答對的題數,將統計結果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六組,得到如下頻率分布直方圖.
六組,得到如下頻率分布直方圖.
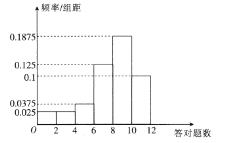
(1)若答對一題得10分,未答對不得分,估計這40人的成績的平均分(同一組中的數據用該組區間的中點值作代表);
(2)若從答對題數在![]() 內的學生中隨機抽取2人,求恰有1人答對題數在
內的學生中隨機抽取2人,求恰有1人答對題數在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年初,新冠肺炎疫情襲擊全國,某省由于人員流動性較大,成為湖北省外疫情最嚴重的省份之一,截至2月29日,該省已累計確診1349例患者(無境外輸入病例).
(1)為了解新冠肺炎的相關特征,研究人員從該省隨機抽取100名確診患者,統計他們的年齡數據,得下面的頻數分布表:
年齡 |
|
|
|
|
|
|
|
|
|
人數 | 2 | 6 | 12 | 18 | 22 | 22 | 12 | 4 | 2 |
由頻數分布表可以大致認為,該省新冠肺炎患者的年齡![]() 服從正態分布img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/11/70cd3e4c/SYS202005251112216152234742_ST/SYS202005251112216152234742_ST.011.png" width="80" height="22" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,其中
服從正態分布img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/11/70cd3e4c/SYS202005251112216152234742_ST/SYS202005251112216152234742_ST.011.png" width="80" height="22" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,其中![]() 近似為這100名患者年齡的樣本平均數(同一組中的數據用該組區間的中點值作代表).請估計該省新冠肺炎患者年齡在70歲以上(
近似為這100名患者年齡的樣本平均數(同一組中的數據用該組區間的中點值作代表).請估計該省新冠肺炎患者年齡在70歲以上(![]() )的患者比例;
)的患者比例;
(2)截至2月29日,該省新冠肺炎的密切接觸者(均已接受檢測)中確診患者約占10%,以這些密切接觸者確診的頻率代替1名密切接觸者確診發生的概率,每名密切接觸者是否確診相互獨立.現有密切接觸者20人,為檢測出所有患者,設計了如下方案:將這20名密切接觸者隨機地按![]() (
(![]() 且
且![]() 是20的約數)個人一組平均分組,并將同組的
是20的約數)個人一組平均分組,并將同組的![]() 個人每人抽取的一半血液混合在一起化驗,若發現新冠病毒,則對該組的
個人每人抽取的一半血液混合在一起化驗,若發現新冠病毒,則對該組的![]() 個人抽取的另一半血液逐一化驗,記
個人抽取的另一半血液逐一化驗,記![]() 個人中患者的人數為
個人中患者的人數為![]() ,以化驗次數的期望值為決策依據,試確定使得20人的化驗總次數最少的
,以化驗次數的期望值為決策依據,試確定使得20人的化驗總次數最少的![]() 的值.
的值.
參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() x2﹣(6+a)x+2alnx(a∈R).
x2﹣(6+a)x+2alnx(a∈R).
(1)討論f(x)的單調性;
(2)函數g(x)![]() x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范圍.
x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產了![]() 兩種產品投放市場,計劃每年對這兩種產品托人200萬元,每種產品一年至少投入20萬元,其中
兩種產品投放市場,計劃每年對這兩種產品托人200萬元,每種產品一年至少投入20萬元,其中![]() 產品的年收益
產品的年收益![]() ,
,![]() 產品的年收益
產品的年收益![]() 與投入
與投入![]() (單位萬元)分別滿足
(單位萬元)分別滿足![]() ;若公司有100名銷售人員,按照對兩種產品的銷售業績分為普銷售、中級銷售以及金牌銷售,其中普銷售28人,中級銷售60人,金牌銷售12人
;若公司有100名銷售人員,按照對兩種產品的銷售業績分為普銷售、中級銷售以及金牌銷售,其中普銷售28人,中級銷售60人,金牌銷售12人
(1)為了使![]() 兩種產品的總收益之和最大,求
兩種產品的總收益之和最大,求![]() 產品每年的投入
產品每年的投入
(2)為了對表現良好的銷售人員進行獎勵,公司制定了兩種獎勵方案:
方案一:按分層抽樣從三類銷售中總共抽取25人給予獎勵:普通銷售獎勵2300元,中級銷售獎勵5000元;金牌銷售獎勵8000元
方案二:每位銷售都參加摸獎游戲,游戲規則:從一個裝有3個白球,2個紅球(求只有顏色不同)的箱子中,有放回地莫三次球,每次只能摸一只球.若摸到紅球的總數為2,則可獎勵1500元,若摸到紅球總數是3,則可獲得獎勵3000元,其他情況不給予獎勵,規定普通銷售均可參加1次摸獎游戲;中級銷售均可參加2次摸獎游戲,金牌銷售均可參加3次摸獎游戲(每次摸獎的結果相互獨立,獎勵疊加)
(ⅰ)求方案一獎勵的總金額;
(ⅱ)假設你是企業老板,試通過計算并結合實際說明,你會選擇哪種方案獎勵銷售員.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定一個數列![]() ,在這個數列里,任取
,在這個數列里,任取![]() 項,并且不改變它們在數列
項,并且不改變它們在數列![]() 中的先后次序,得到的數列稱為數列
中的先后次序,得到的數列稱為數列![]() 的一個
的一個![]() 階子數列.
階子數列.
已知數列![]() 的通項公式為
的通項公式為![]() (
(![]() 為常數),等差數列
為常數),等差數列![]() 是
是
數列![]() 的一個3階子數列.
的一個3階子數列.
(1)求![]() 的值;
的值;
(2)等差數列![]() 是
是![]() 的一個
的一個![]() 階子數列,且
階子數列,且
![]() (
(![]() 為常數,
為常數,![]() ,求證:
,求證:![]() ;
;
(3)等比數列![]() 是
是![]() 的一個
的一個![]() 階子數列,
階子數列,
求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點![]() ,焦點在
,焦點在![]() 軸上,離心率為
軸上,離心率為![]() 的橢圓過點
的橢圓過點![]()

(1)求橢圓的方程;
(2)設不過原點![]() 的直線
的直線![]() 與該橢圓交于
與該橢圓交于![]() 兩點,滿足直線
兩點,滿足直線![]() 的斜率依次成等比數列,求
的斜率依次成等比數列,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:①有的質數是偶數;②存在正整數![]() ,使得
,使得![]() 為
為![]() 的約數;③有的三角形三個內角成等差數列;④與給定的圓只有一個公共點的直線是圓的切線.其中既是存在性命題又是真命題的個數為( )
的約數;③有的三角形三個內角成等差數列;④與給定的圓只有一個公共點的直線是圓的切線.其中既是存在性命題又是真命題的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com