【題目】某城市交通部門為了對該城市共享單車加強監(jiān)管，隨機選取了100人就該城市共享單車的推行情況進行問卷調(diào)查，并將問卷中的這100人根據(jù)其滿意度評分值（百分制）按照
，
，
，
，
分成5組，制成如圖所示頻率分直方圖.
（1）求圖中
的值及這組數(shù)據(jù)的眾數(shù)；
（2）已知滿意度評分值在內(nèi)的男生數(shù)與女生數(shù)的比為
，若在滿意度評分值為的人中隨機抽取2人進行座談，求2人均為男生的概率.
【答案】（1）
，眾數(shù)為75；（2）
【解析】
（1）根據(jù)小矩形面積和為1，求解
，根據(jù)最高小矩形的組中值為眾數(shù)，求解即可.
（2）先根據(jù)頻率分布直方圖求解在
內(nèi)有5人，其中男生3人，女生2人，記為
，
，
，
，
，古典概型概率公式，求解即可.
（1）由
，解得.這組數(shù)據(jù)的眾數(shù)為75.
（2）滿意度評分值在內(nèi)有
人.
其中男生3人，女生2人，記為，，，，.
記滿意度評分值為的人中隨機抽取2人進行座談，恰有1名女生為事件
.
總基本事件空間為：
則總基本事件個數(shù)為10個，包含的基本事件個數(shù)為3個.
根據(jù)古典概型概率公式可知.
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知橢圓
：
，設(shè)
是橢圓上任一點，從原點
向圓
：
作兩條切線，分別交橢圓于點
，
.
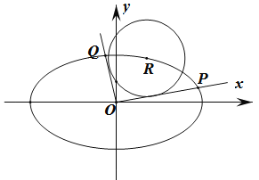
（1）若直線
，
互相垂直，且圓心落在第一象限，求圓的圓心坐標；
（2）若直線，的斜率都存在，并記為
，
.
①求證：
；
②試問
是否為定值？若是，求出該定值；若不是，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的右焦點
與拋物線
的焦點重合，且橢圓的離心率為
．
（1）求橢圓的標準方程；
（2）過橢圓
右焦點的直線
與橢圓交于兩點
、
，在
軸上是否存在點
，使得
為定值？若存在，求出點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在一次體育興趣小組的聚會中，要安排6人的座位，使他們在如圖所示的6個椅子中就坐，且相鄰座位(如1與2，2與3)上的人要有共同的體育興趣愛好．現(xiàn)已知這6人的體育興趣愛好如下表所示，且小林坐在1號位置上，則4號位置上坐的是
小林 | 小方 | 小馬 | 小張 | 小李 | 小周 | |
體育興趣愛好 | 籃球，網(wǎng)球，羽毛球 | 足球，排球，跆拳道 | 籃球，棒球，乒乓球 | 擊劍，網(wǎng)球，足球 | 棒球，排球，羽毛球 | 跆拳道，擊劍，自行車 |
A.小方B.小張C.小周D.小馬
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】唐三彩是中國古代陶瓷燒制工藝的珍品，它吸取了中國國畫、雕塑等工藝美術(shù)的特點，在中國文化中占有重要的歷史地位，在陶瓷史上留下了濃墨重彩的一筆.唐三彩的生產(chǎn)至今已有1300多年的歷史，制作工藝十分復雜，而且優(yōu)質(zhì)品檢驗異常嚴格，檢驗方案是：先從燒制的這批唐三彩中任取 3件作檢驗，這3件唐三彩中優(yōu)質(zhì)品的件數(shù)記為
.如果
，再從這批唐三彩中任取3件作檢驗，若都為優(yōu)質(zhì)品，則這批唐三彩通過檢驗；如果
，再從這批唐三彩中任取1件作檢驗，若為優(yōu)質(zhì)品，則這批唐三彩通過檢驗；其他情況下，這批唐三彩都不能通過檢驗.假設(shè)這批唐三彩的優(yōu)質(zhì)品概率為
，即取出的每件唐三彩是優(yōu)質(zhì)品的概率都為，且各件唐三彩是否為優(yōu)質(zhì)品相互獨立.
（1）求這批唐三彩通過優(yōu)質(zhì)品檢驗的概率；
（2）已知每件唐三彩的檢驗費用為100元，且抽取的每件唐三彩都需要檢驗，對這批唐三彩作質(zhì)量檢驗所需的總費用記為
元，求的分布列及數(shù)學期望.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知等比數(shù)列{an}的前n項和為Sn，公比q＞0，S2=2a2-2，S3=a4-2，數(shù)列{an}滿足a2=4b1，nbn+1-（n+1）bn=n2+n，（n∈N*）.
（1）求數(shù)列{an}的通項公式；
（2）證明數(shù)列{
}為等差數(shù)列；
（3）設(shè)數(shù)列{cn}的通項公式為：Cn=
，其前n項和為Tn，求T2n.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】光伏發(fā)電是利用太陽能電池及相關(guān)設(shè)備將太陽光能直接轉(zhuǎn)化為電能．近幾年在國內(nèi)出臺的光伏發(fā)電補貼政策的引導下，某地光伏發(fā)電裝機量急劇上漲，如下表：
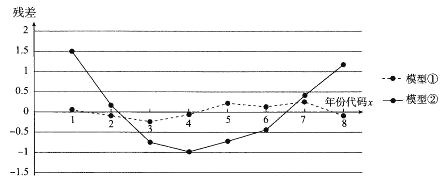
某位同學分別用兩種模型：①
②
進行擬合，得到相應的回歸方程并進行殘差分析，殘差圖如下(注：殘差等于
)：
經(jīng)過計算得
，
．
(1)根據(jù)殘差圖，比較模型①，②的擬合效果，應該選擇哪個模型?并簡要說明理由．
(2)根據(jù)(1)的判斷結(jié)果及表中數(shù)據(jù)建立y關(guān)于x的回歸方程，并預測該地區(qū)2020年新增光伏裝機量是多少．(在計算回歸系數(shù)時精確到0.01)
附：歸直線的斜率和截距的最小二乘估計公式分別為：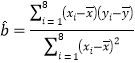
，
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖所示，已知點
，過點
作直線
、
與圓
：
和拋物線
：
都相切.
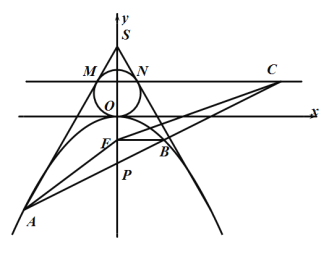
（1）求拋物線的兩切線的方程；
（2）設(shè)拋物線的焦點為
，過點
的直線與拋物線相交于
、
兩點，與拋物線的準線交于點（其中點靠近點），且
，求
與
的面積之比.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
