Question

設變量x，y滿足

x+y≤1 x-y≤1 y≥0

，則x+2y的最大值為（　　）

A．1

B．2

C．3

D．-2

Answer 1

分析：先畫出約束條件

x+y≤1 x-y≤1 y≥0

的可行域，再求出可行域中各角點的坐標，將各點坐標代入目標函數的解析式，分析后易得目標函數z=x+2y的最大值．

解答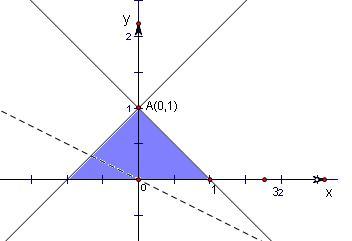：解：由約束條件

x+y≤1 x-y≤1 y≥0

得如圖所示的三角形區域，
三個頂點坐標為A（0，1），（-1，0），C（1，0）
將三個代入得z的值分別為2，-1，1．
直線z=x+2y過點 A（0，1）時，z取得最大值為2；
故選B．

點評：在解決線性規劃的小題時，我們常用“角點法”，其步驟為：①由約束條件畫出可行域⇒②求出可行域各個角點的坐標⇒③將坐標逐一代入目標函數⇒④驗證，求出最優解．