
在平面直角坐標系![]() O
O![]() 中,直線
中,直線![]() 與拋物線
與拋物線![]() =2
=2![]() 相交于A、B兩點.
相交于A、B兩點.

(1)求證:“如果直線![]() 過點T(3,0),那么
過點T(3,0),那么![]()
![]() =3”是真命題;
=3”是真命題;
(2)寫出(1)中命題的逆命題,判斷它是真命題還是假命題,并說明理由.
證明:(1)設過點T(3,0)的直線l交拋物線y2=2x于點A(x1,y1)、B(x12,y2).
①當直線l的斜率下存在時,L:x=3,
此時L與拋物線相交于點A(3,![]() )、B(3,-
)、B(3,-![]() ).∴
).∴![]() =3
=3
②當直線l的斜率存在時,設直線l的方程為y=k(x-3),其中k≠0.
![]() 得
得![]()

又∵x1=![]() y
y![]() , x2=
, x2=![]() y
y![]() , ∴
, ∴![]() =x1x2+y1y2=
=x1x2+y1y2=![]() =3.
=3.
綜上所述, 命題“如果直線l過點T(3,0),那么![]() =3”是真命題.
=3”是真命題.
或者設直線為x=my+3那么就不必討論斜率是否存在
(2)逆命題是:設直線l交拋物線y2=2x于A、B兩點,如果![]() =3,那么該直線過點T(3,0).
=3,那么該直線過點T(3,0).
例如:取拋物線上的點A(2,2),B(![]() ,1),此時
,1),此時![]() =3,
=3,
直線AB的方程為y=![]() (x+1),而T(3,0)不在直線AB上.
(x+1),而T(3,0)不在直線AB上.
該命題是假命題.
說明:由拋物線y2=2x上的點A(x1,y1)、B(x12,y2)滿足![]() =3,可得y1y2=-6.
=3,可得y1y2=-6.
或y1y2=2,如果y1y2=-6.,可證得直線AB過點(3,0);如果y1y2=2, 可證得直線AB過點(-1,0),而不過點(3,0).


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案科目:高中數學 來源:2014屆黑龍江省高二上學期期末理科數學試卷(解析版) 題型:解答題
(本題12分)在平面直角坐標系 O
O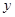 中,直線
中,直線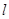 與拋物線
與拋物線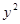 =2
=2 相交于A、B兩點。
相交于A、B兩點。
(1)求證:命題“如果直線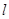 過點T(3,0),那么
過點T(3,0),那么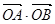 =3”是真命題;
=3”是真命題;
(2)寫出(1)中命題的逆命題,判斷它是真命題還是假命題,并說明理由。
查看答案和解析>>
科目:高中數學 來源:2014屆山東省濟寧市高二上學期期末理科數學(解析版) 題型:解答題
在平面直角坐標系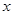 O
O 中,直線
中,直線 與拋物線
與拋物線 =2
=2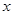 相交于A、B兩點。
相交于A、B兩點。
(1)求證:命題“如果直線 過點T(3,0),那么
過點T(3,0),那么 =3”是真命題;
=3”是真命題;
(2)寫出(1)中命題的逆命題,判斷它是真命題還是假命題,并說明理由。
查看答案和解析>>
科目:高中數學 來源:2014屆福建南安一中高二上學期期中考試理科數學試卷(解析版) 題型:解答題
(12分)在平面直角坐標系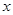 O
O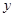 中,直線
中,直線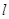 與拋物線
與拋物線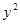 =2
=2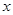 相交于A、B兩點.
相交于A、B兩點.
(Ⅰ)求證:命題“如果直線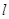 過點T(3,0),那么
過點T(3,0),那么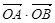 =3”是真命題;
=3”是真命題;
(Ⅱ)寫出(1)中命題的逆命題,判斷它是真命題還是假命題,并說明理由.
查看答案和解析>>
科目:高中數學 來源:2010年浙江省高二上學期期中考試數學理卷 題型:解答題
(10分)在平面直角坐標系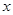 O
O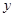 中,直線
中,直線 與拋物線
與拋物線 相交于
相交于 、
、 兩點。
兩點。
(Ⅰ)求證:“如果直線 過點
過點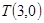 ,那么
,那么
 =
= ”是真命題;
”是真命題;
(Ⅱ)寫出(1)中命題的逆命題,判斷它是真命題還是假命題,并說明理由。
查看答案和解析>>
科目:高中數學 來源:2012屆遼寧省大連市高二上學期期末考試(文科)試題 題型:解答題
在平面直角坐標系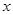 O
O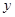 中,直線
中,直線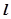 與拋物線
與拋物線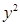 =2
=2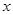 相交于A、B兩點.
相交于A、B兩點.
(1)求證:“如果直線 過點T(3,0),那么
過點T(3,0),那么
 =3”是真命題;
=3”是真命題;
(2)寫出(1)中命題的逆命題,判斷它是真命題還是假命題,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com