
【題目】為振興旅游業,四川省2009年面向國內發行總量為2000萬張的熊貓優惠卡,向省外人士發行的是熊貓金卡(簡稱金卡),向省內人士發行的是熊貓銀卡(簡稱銀卡).某旅游公司組織了一個有36名游客的旅游團到四川名勝旅游,其中 ![]() 是省外游客,其余是省內游客.在省外游客中有
是省外游客,其余是省內游客.在省外游客中有 ![]() 持金卡,在省內游客中有
持金卡,在省內游客中有 ![]() 持銀卡.
持銀卡.
(Ⅰ)在該團中隨機采訪3名游客,求恰有1人持金卡且持銀卡者少于2人的概率;
(Ⅱ)在該團的省內游客中隨機采訪3名游客,設其中持銀卡人數為隨機變量ξ,求ξ的分布列及數學期望Eξ.
【答案】解:(Ⅰ)由題意得,省外游客有27人,其中9人持金卡;省內游客有9人,其中6人持銀卡.設事件B為“采訪該團3人中,恰有1人持金卡且持銀卡者少于2人”, 事件A1為“采訪該團3人中,1人持金卡,0人持銀卡”,
事件A2為“采訪該團3人中,1人持金卡,1人持銀卡”.
P(B)=P(A1)+P(A2)
= ![]() +
+ ![]()
= ![]() =
= ![]() .
.
所以在該團中隨機采訪3人,恰有1人持金卡且持銀卡者少于2人的概率是 ![]() .
.
(Ⅱ)ξ的可能取值為0,1,2,3,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以ξ的分布列為
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以 ![]() .
.
【解析】(Ⅰ)由題意得,境外游客有27人,其中9人持金卡;境內游客有9人,其中6人持銀卡.記出事件,表示出事件的概率,根據互斥事件的概率公式,得到結論.(Ⅱ)ξ的可能取值為0,1,2,3,分別求出其對應的概率,能得到ξ的分布列和數學期望Eξ.


科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,棱AB的中點為P,若光線從點P出發,依次經三個側面BCC1B1 , DCC1D1 , ADD1A1反射后,落到側面ABB1A1(不包括邊界),則入射光線PQ與側面BCC1B1所成角的正切值的范圍是( ) 
A.( ![]() ,
, ![]() )
)
B.( ![]() ,4)
,4)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心在![]() 軸非負半軸上,半徑為2的圓C與直線
軸非負半軸上,半徑為2的圓C與直線![]() 相切.
相切.
(1)求圓C的方程;
(2)設不過原點O的直線l與圓O:x2+y2=4相交于不同的兩點A,B.①求△OAB的面積的最大值;②在圓C上,是否存在點M(m,n),使得直線l的方程為mx+ny=1,且此時△OAB的面積恰好取到①中的最大值?若存在,求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
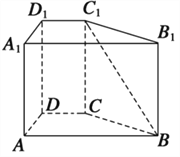
【題目】如圖,已知直四棱柱ABCD—A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A為直角,AB∥CD,AB=4,AD=2,DC=2.
(Ⅰ)求線段BC1的長度;
(Ⅱ)異面直線BC1與DC所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某養殖廠需定期購買飼料,已知該廠每天需要飼料200 kg,每千克飼料的價格為1.8元,飼料的保管與其他費用為平均每千克每天0.03元,購買飼料每次支付運費300元.
(1)該廠多少天購買一次飼料才能使平均每天支付的總費用最少?
(2)若提供飼料的公司規定:當一次購買飼料不少于5 t時其價格可享受八五折優惠(即為原價的85%).該廠是否可以考慮利用此優惠條件?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com