
【題目】已知函數![]() 有兩個不同的極值點x1,x2,且x1<x2.
有兩個不同的極值點x1,x2,且x1<x2.
(1)求實數a的取值范圍;
(2)求證:x1x2<a2.
【答案】(1)(e,+∞);(2)見解析
【解析】
(1)先求導數,再根據導函數有兩個不同的零點,確定實數a所需滿足的條件,解得結果,(2)先根據極值點解得a,再代入化簡不等式x1x2<a2,設![]() ,構造一元函數,利用導數研究函數單調性,最后構造單調性證明不等式.
,構造一元函數,利用導數研究函數單調性,最后構造單調性證明不等式.
(1)∵函數![]() ,∴x>0,f′(x)=x-alnx,
,∴x>0,f′(x)=x-alnx,
∵函數![]() 有兩個不同的極值點x1,x2,且x1<x2.
有兩個不同的極值點x1,x2,且x1<x2.
∴f′(x)=x-alnx=0有兩個不等根,
令g(x)=x-alnx,則![]() =
=![]() ,(x>0),
,(x>0),
①當a≤0時,得g′(x)>0,則g(x)在(0,+∞)上單調遞增,
∴g(x)在(0,+∞)上不可能有兩個零點.
②當a>0時,由g′(x)>0,解得x>a,由g′(x)<0,解得0<x<a,
則g(x)在(0,a)上單調遞減,在(a,+∞)上單調遞增,
要使函數g(x)有兩個零點,則g(a)=a-alna<0,
解得a>e,∴實數a的取值范圍是(e,+∞).
(2)由x1,x2是g(x)=x-alnx=0的兩個根,
則 ,兩式相減,得a(lnx2-lnx1)=x2-x1),
,兩式相減,得a(lnx2-lnx1)=x2-x1),
即a=![]() ,即證x1x2<
,即證x1x2<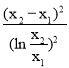 ,
,
即證![]() =
=![]() ,
,
由x1<x2,得![]() =t>1,只需證ln2t-t-
=t>1,只需證ln2t-t-![]() ,
,
設g(t)=ln2t-t-![]() ,則g′(t)=
,則g′(t)=![]() =
=![]() ,
,
令h(t)=2lnt-t+![]() ,∴h′(t)=
,∴h′(t)=![]() =-(
=-(![]() )2<0,
)2<0,
∴h(t)在(1,+∞)上單調遞減,∴h(t)<h(1)=0,
∴g′(t)<0,即g(t)在(1,+∞)上是減函數,∴g(t)<g(1)=0,
即ln2t<t-2+![]() 在(1,+∞)上恒成立,∴x1x2<a2.
在(1,+∞)上恒成立,∴x1x2<a2.


科目:高中數學 來源: 題型:
【題目】某工廠抽取了一臺設備![]() 在一段時間內生產的一批產品,測量一項質量指標值,繪制了如圖所示的頻率分布直方圖.
在一段時間內生產的一批產品,測量一項質量指標值,繪制了如圖所示的頻率分布直方圖.

(1)計算該樣本的平均值![]() ,方差
,方差![]() ;(同一組中的數據用該組區間的中點值作代表)
;(同一組中的數據用該組區間的中點值作代表)
(2)根據長期生產經驗,可以認為這臺設備在正常狀態下生產的產品的質量指標值服從正態分布![]() ,其中
,其中![]() 近似為樣本平均值,
近似為樣本平均值,![]() 近似為樣本方差
近似為樣本方差![]() .任取一個產品,記其質量指標值為
.任取一個產品,記其質量指標值為![]() .若
.若![]() ,則認為該產品為一等品;
,則認為該產品為一等品;![]() ,則認為該產品為二等品;若
,則認為該產品為二等品;若![]() ,則認為該產品為不合格品.已知設備
,則認為該產品為不合格品.已知設備![]() 正常狀態下每天生產這種產品1000個.
正常狀態下每天生產這種產品1000個.
(i)用樣本估計總體,問該工廠一天生產的產品中不合格品是否超過![]() ?
?
(ii)某公司向該工廠推出以舊換新活動,補足50萬元即可用設備![]() 換得生產相同產品的改進設備
換得生產相同產品的改進設備![]() .經測試,設備
.經測試,設備![]() 正常狀態下每天生產產品1200個,生產的產品為一等品的概率是
正常狀態下每天生產產品1200個,生產的產品為一等品的概率是![]() ,二等品的概率是
,二等品的概率是![]() ,不合格品的概率是
,不合格品的概率是![]() .若工廠生產一個一等品可獲得利潤50元,生產一個二等品可獲得利潤30元,生產一個不合格品虧損40元,試為工廠做出決策,是否需要換購設備
.若工廠生產一個一等品可獲得利潤50元,生產一個二等品可獲得利潤30元,生產一個不合格品虧損40元,試為工廠做出決策,是否需要換購設備![]() ?
?
參考數據:①![]() ;②
;②![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() ,點A,B分別是橢圓E的左頂點和上頂點,直線AB與圓C:x2+y2=c2相離,其中c是橢圓的半焦距,P是直線AB上一動點,過點P作圓C的兩條切線,切點分別為M,N,若存在點P使得△PMN是等腰直角三角形,則橢圓離心率平方e2的取值范圍是_____.
,點A,B分別是橢圓E的左頂點和上頂點,直線AB與圓C:x2+y2=c2相離,其中c是橢圓的半焦距,P是直線AB上一動點,過點P作圓C的兩條切線,切點分別為M,N,若存在點P使得△PMN是等腰直角三角形,則橢圓離心率平方e2的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,將曲線
,將曲線![]() 向左平移
向左平移![]() 個單位長度得到曲線
個單位長度得到曲線![]() .
.
(1)求曲線![]() 的參數方程;
的參數方程;
(2)已知![]() 為曲線
為曲線![]() 上的動點,
上的動點, ![]() 兩點的極坐標分別為
兩點的極坐標分別為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據氣象局統計,某市2019年從1月1日至1月30日這30天里有26天出現霧霾天氣.國際上通常用環境空氣質量指數(AQI)來描述污染狀況,下表是某氣象觀測點記錄的連續4天里,該市AQI指數![]() 與當天的空氣水平可見度
與當天的空氣水平可見度![]() 的情況.
的情況.
AQI指數 | 900 | 700 | 300 | 100 |
空氣水平可見度 | 0.5 | 3.5 | 6.5 | 9.5 |
(1)設![]() ,根據表中的數據,求出
,根據表中的數據,求出![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)若某天該市AQT指數![]() ,那么當天空氣水平可見度大約為多少?
,那么當天空氣水平可見度大約為多少?
附:參考數據:![]() ,
,![]() .
.
參考公式:線性回歸力程![]() 中,
中,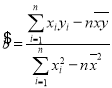 ,
,![]() ,其中
,其中![]() 為樣本平均數.
為樣本平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x-1|+|x+m|.
(l)當m=l時,解不等式f(x)≥3;
(2)證明:對任意x∈R,2f(x)≥|m+1|-|m|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,已知每售出一箱酸奶的利潤為50元,當天未售出的酸奶降價處理,以每箱虧損10元的價格全部處理完.若供不應求,可從其它商店調撥,每銷售1箱可獲利30元.假設該超市每天的進貨量為14箱,超市的日利潤為![]() 元.為確定以后的訂購計劃,統計了最近50天銷售該酸奶的市場日需求量,其頻率分布表如圖所示.
元.為確定以后的訂購計劃,統計了最近50天銷售該酸奶的市場日需求量,其頻率分布表如圖所示.
序號 | 分組 | 頻數(天) | 頻率 |
1 |
|
| 0.16 |
2 |
| 12 |
|
3 |
|
| 0.3 |
4 |
|
|
|
5 |
| 5 | 0.1 |
合計 | 50 | 1 | |
(1)求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 關于日需求量
關于日需求量![]() 的函數表達式;
的函數表達式;
(3)以50天記錄的酸奶需求量的頻率作為酸奶需求量發生的概率,估計日利潤在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 若對任意的實數x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,則實數m的取值范圍是( )
若對任意的實數x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,則實數m的取值范圍是( )
A.[1,4)B.(1,4)C.(![]() )D.[
)D.[![]() ]
]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com