
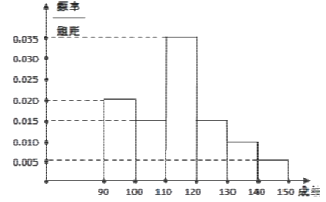
【題目】某校高三數(shù)學競賽初賽考試結(jié)束后,對考生成績進行統(tǒng)計(考生成績均不低于90分,滿分150分),將成績按如下方式分為六組,第一組.如圖為其頻率分布直方圖的一部分,若第四、五、六組的人數(shù)依次成等差數(shù)列,且第六組有4人. 
(1)請補充完整頻率分布直方圖,并估計這組數(shù)據(jù)的平均數(shù)M;
(2)現(xiàn)根據(jù)初賽成績從第四組和第六組中任意選2人,記他們的成績分別為x,y.若|x﹣y|≥10,則稱此二人為“黃金幫扶組”,試求選出的二人為“黃金幫扶組”的概率P1;
(3)以此樣本的頻率當作概率,現(xiàn)隨機在這組樣本中選出3名學生,求成績不低于120分的人數(shù)ξ的分布列及期望.
【答案】
(1)解:頻率分布直方圖見解析,
M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5
(2)解:依題意可得:第四組人數(shù)為:
![]() =12,
=12,
故P1= ![]() =
= ![]()
(3)解:依題意可得:樣本總?cè)藬?shù)為: ![]() =80,成績不低于120分的人數(shù)為:80×(0.05+0.10+0.15)=24,故在樣本中任選1人,其成績不低于120分的概率=
=80,成績不低于120分的人數(shù)為:80×(0.05+0.10+0.15)=24,故在樣本中任選1人,其成績不低于120分的概率= ![]() =
= ![]() .由已知ξ的可能取值為0,1,2,3.
.由已知ξ的可能取值為0,1,2,3.
ξ~B ![]() ,P(ξ=0)=
,P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() .ξ的分布列如下
.ξ的分布列如下
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故Eξ= ![]() =
= ![]() .
.
【解析】(1)利用頻率分布直方圖的性質(zhì)即可得出.(2)依題意可得:第四組人數(shù)為: ![]() =12,可得P1=
=12,可得P1= ![]() .(3)依題意可得:樣本總?cè)藬?shù)為:
.(3)依題意可得:樣本總?cè)藬?shù)為: ![]() =80,成績不低于120分的人數(shù)為:80×(0.05+0.10+0.15)=24,故在樣本中任選1人,其成績不低于120分的概率=
=80,成績不低于120分的人數(shù)為:80×(0.05+0.10+0.15)=24,故在樣本中任選1人,其成績不低于120分的概率= ![]() =
= ![]() .由已知ξ的可能取值為0,1,2,3.ξ~B
.由已知ξ的可能取值為0,1,2,3.ξ~B ![]() ,即可得出.
,即可得出.
【考點精析】通過靈活運用頻率分布直方圖,掌握頻率分布表和頻率分布直方圖,是對相同數(shù)據(jù)的兩種不同表達方式.用緊湊的表格改變數(shù)據(jù)的排列方式和構(gòu)成形式,可展示數(shù)據(jù)的分布情況.通過作圖既可以從數(shù)據(jù)中提取信息,又可以利用圖形傳遞信息即可以解答此題.


 天天練口算系列答案
天天練口算系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 是定義在
是定義在![]() 上的偶函數(shù),當
上的偶函數(shù),當![]() 時,
時,![]() .
.
(1)直接寫出函數(shù)![]() 的增區(qū)間(不需要證明);
的增區(qū)間(不需要證明);
(2)求出函數(shù)![]() ,
,![]() 的解析式;
的解析式;
(3)若函數(shù)![]() ,
,![]() ,求函數(shù)
,求函數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)y=f″(x)是y=f′(x)的導數(shù).某同學經(jīng)過探究發(fā)現(xiàn),任意一個三次函數(shù)f(x)=ax3+bx2+cx+d(a≠0)都有對稱中心(x0 , f(x0)),其中x0滿足f″(x0)=0.已知f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,則f(
,則f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )=( )
)=( )
A.2013
B.2014
C.2015
D.2016
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,已知點A的極坐標為( ![]() ,
, ![]() ),直線l的極坐標方程為ρcos(θ﹣
),直線l的極坐標方程為ρcos(θ﹣ ![]() )=a,且點A在直線l上,
)=a,且點A在直線l上,
(1)求a的值及直線l的直角坐標方程;
(2)圓C的參數(shù)方程為 ![]() (α為參數(shù)),試判斷直線l與圓C的位置關(guān)系.
(α為參數(shù)),試判斷直線l與圓C的位置關(guān)系.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若關(guān)于x的不等式xex﹣2ax+a<0的非空解集中無整數(shù)解,則實數(shù)a的取值范圍是( )
A.[ ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() )
)
C.[ ![]() ,e]
,e]
D.[ ![]() ,e]
,e]
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)![]() 是雙曲線
是雙曲線![]() 上一點,
上一點, ![]() ,
, ![]() 分別是雙曲線左、右兩個焦點,若
分別是雙曲線左、右兩個焦點,若![]() ,則
,則![]() 等于( )
等于( )
A. 1 B. 17 C. 1或17 D. 以上答案均不對
【答案】B
【解析】根據(jù)雙曲線的定義得到![]() 根據(jù)雙曲線的焦半徑的范圍得到
根據(jù)雙曲線的焦半徑的范圍得到![]() 故結(jié)果為17.
故結(jié)果為17.
故答案為:B。
【題型】單選題
【結(jié)束】
10
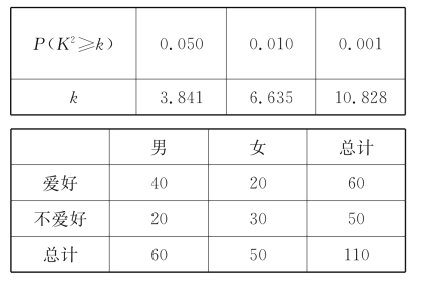
【題目】某中學學生會為了調(diào)查愛好游泳運動與性別是否有關(guān),通過隨機詢問110名性別不同的高中生是否愛好游泳運動得到如下的列聯(lián)表:由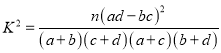 并參照附表,得到的正確結(jié)論是( )
并參照附表,得到的正確結(jié)論是( )
A. 在犯錯誤的概率不超過![]() 的前提下,認為“愛好游泳運動與性別有關(guān)”
的前提下,認為“愛好游泳運動與性別有關(guān)”
B. 在犯錯誤的概率不超過![]() 的前提下,認為“愛好游泳運動與性別無關(guān)”
的前提下,認為“愛好游泳運動與性別無關(guān)”
C. 有![]() 的把握認為“愛好游泳運動與性別有關(guān)”
的把握認為“愛好游泳運動與性別有關(guān)”
D. 有![]() 的把握認為“愛好游泳運動與性別無關(guān)”
的把握認為“愛好游泳運動與性別無關(guān)”
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知a∈R,函數(shù)f(x)=ln(x+a)﹣x,曲線y=f(x)與x軸相切. (Ⅰ)求f(x)的單調(diào)區(qū)間;
(Ⅱ)是否存在實數(shù)m使得 ![]() 恒成立?若存在,求實數(shù)m的值;若不存在,說明理由.
恒成立?若存在,求實數(shù)m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】最新公布的《道路交通安全法》和《道路交通安全法實施條例》對車速、安全車距以及影響駕駛?cè)朔磻?yīng)快慢等因素均有詳細規(guī)定,這些規(guī)定說到底主要與剎車距離有關(guān),剎車距離是指從駕駛員發(fā)現(xiàn)障礙到制動車輛,最后完全停止所行駛的距離,即:剎車距離=反應(yīng)距離+制動距離,反應(yīng)距離=反應(yīng)時間×速率,制動距離與速率的平方成正比,某反應(yīng)時間為![]() 的駕駛員以
的駕駛員以![]() 的速率行駛,遇緊急情況,汽車的剎車距離為
的速率行駛,遇緊急情況,汽車的剎車距離為![]() .
.
(![]() )試將剎車距離
)試將剎車距離![]() 表示為速率
表示為速率![]() 的函數(shù).
的函數(shù).
(![]() )若該駕駛員駕駛汽車在限速為
)若該駕駛員駕駛汽車在限速為![]() 的公路上行駛,遇緊急情況,汽車的剎車距離為
的公路上行駛,遇緊急情況,汽車的剎車距離為![]() ,試問該車是否超速?請說明理由.
,試問該車是否超速?請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
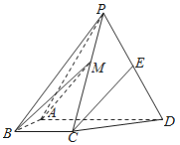
【題目】如圖,四棱錐![]() 中,側(cè)面
中,側(cè)面![]() 為等邊三角形且垂直于底面
為等邊三角形且垂直于底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中點.
中點.
(1)證明:直線![]() 平面
平面![]() ;
;
(2)點![]() 在棱
在棱![]() 上,且直線
上,且直線![]() 與底面
與底面![]() 所成角為
所成角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com