
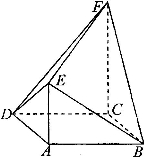
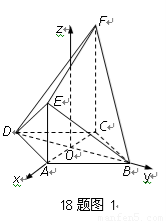
如圖,菱形ABCD中,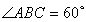 ,
,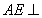 平面ABCD,
平面ABCD,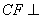 平面ABCD,
平面ABCD,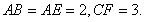
(1)求證: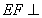 平面BDE;
平面BDE;
(2)求銳二面角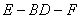 的大小.
的大小.
(1)證明:見解析;(2)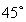 .
.
【解析】
試題分析:(1)利用已有的垂直關系,以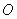 為原點,
為原點, ,
, 為
為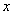 、
、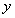 軸正向,
軸正向,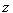 軸過
軸過 且平行于
且平行于 ,建立空間直角坐標系通過計算
,建立空間直角坐標系通過計算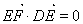 ,
,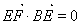 ,得到
,得到 ,
,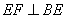 ,
,
達到證明目的.
(2)由知(1)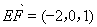 是平面
是平面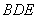 的一個法向量,
的一個法向量,
設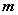
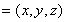 是平面
是平面 的一個法向量,利用
的一個法向量,利用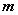
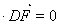 ,
, 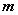
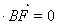
確定得到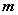
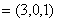 ,由
,由 <
<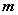 ,
, >
>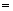 及二面角
及二面角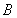 —
—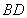 —
—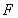 為銳二面角,得解.
為銳二面角,得解.
“向量法”往往能將復雜的證明問題,轉化成計算問題,達到化繁為簡,化難為易的目的.
試題解析:(1)證明:連接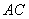 、
、 ,設
,設 ,
,
∵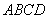 為菱形,∴
為菱形,∴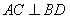 ,以
,以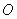 為原點,
為原點, ,
, 為
為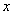 、
、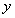 軸正向,
軸正向,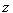 軸過
軸過 且平行于
且平行于 ,建立空間直角坐標系(圖1), 2分
,建立空間直角坐標系(圖1), 2分
則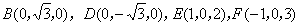 ,
,
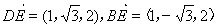 ,
,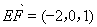 , 4分
, 4分
∴ 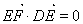 ,
,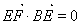 ,∴
,∴ ,
,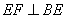 ,
,
又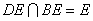 ,∴
,∴ ⊥平面
⊥平面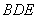 . 6分
. 6分
(2)由知(1)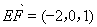 是平面
是平面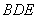 的一個法向量,
的一個法向量,
設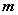
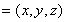 是平面
是平面 的一個法向量,
的一個法向量,
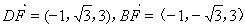 ,由
,由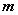
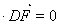 ,
, 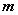
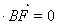

得: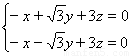 , 8分
, 8分
取 ,得
,得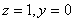 ,于是
,于是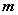
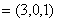
 <
<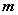 ,
, >
>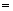
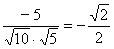 10分
10分
但二面角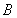 —
—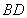 —
—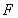 為銳二面角,
為銳二面角,
故其大小為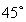 . 12分
. 12分
考點:垂直關系,二面角的計算,空間向量的應用.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案科目:高中數學 來源: 題型:
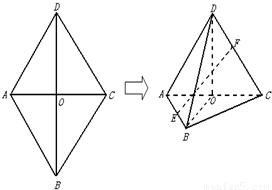
 (2012•閘北區二模)如圖,菱形ABCD中,AB=AC=1,其對角線的交點為O,現將△ADC沿對角線AC向上翻折,使得OD⊥OB.在四面體ABCD中,E在AB上移動,點F在DC上移動,且AE=CF=a(0≤a≤1).
(2012•閘北區二模)如圖,菱形ABCD中,AB=AC=1,其對角線的交點為O,現將△ADC沿對角線AC向上翻折,使得OD⊥OB.在四面體ABCD中,E在AB上移動,點F在DC上移動,且AE=CF=a(0≤a≤1).查看答案和解析>>
科目:高中數學 來源: 題型:
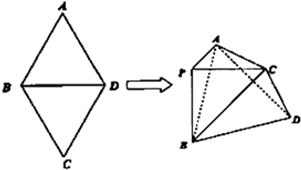 如圖,菱形ABCD中,∠A=60°,把菱形ABCD沿對角線BD折成二面角A-BD-C,AC=BD,空間中的點P滿足PA、PB、PC兩兩垂直,則下列命題中錯誤的是( )
如圖,菱形ABCD中,∠A=60°,把菱形ABCD沿對角線BD折成二面角A-BD-C,AC=BD,空間中的點P滿足PA、PB、PC兩兩垂直,則下列命題中錯誤的是( )查看答案和解析>>
科目:高中數學 來源: 題型:
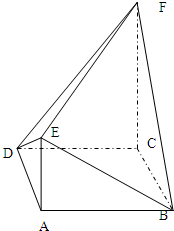 (2012•湘潭模擬)如圖,菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.
(2012•湘潭模擬)如圖,菱形ABCD中,∠ABC=60°,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,CF=3.查看答案和解析>>
科目:高中數學 來源:2012年上海市閘北區高考數學二模試卷(理科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com