
某中學經市批準建設分校,工程從2010年底開工到2013年底完工,分三期完成,經過初步招標淘汰后,確定由甲、乙兩建筑公司承建,且每期工程由兩公司之一獨立完成,必須在建完前一期工程后再建后一期工程,已知甲公司獲得第一期,第二期,第三期工程承包權的概率分別是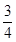 ,
,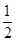 ,
,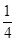 .
.
(I)求甲乙兩公司均至少獲得l期工程的概率;
(II)求甲公司獲得的工程期數的分布列和數學期望E(X).
(I)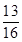 ;
;
(II)分布列為
0 1 2 3 
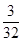
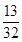
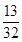
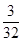
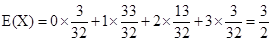 .
.
解析試題分析:(I)由題意得乙公司得第一期,第二期,第三期工程承包權的概率分別是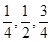 .記“甲乙至少獲得1期工程”為事件
.記“甲乙至少獲得1期工程”為事件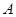 ,甲公司獲得1期工程,乙公司獲得2期工程為事件
,甲公司獲得1期工程,乙公司獲得2期工程為事件 ,甲公司獲得2期工程,乙公司獲得1期工程為事件
,甲公司獲得2期工程,乙公司獲得1期工程為事件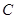 .
.
利用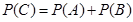 或
或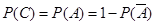 加以計算;
加以計算;
(II)由題意知,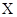 可取
可取 ,
,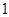 ,
,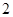 ,
,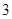 .利用相互獨立事件同時發生的概率計算公式即得.
.利用相互獨立事件同時發生的概率計算公式即得.
應用數學期望計算公式得 .
.
此類問題的解答,關鍵在于明確算理,細心計算.
試題解析:(I)由題意得乙公司得第一期,第二期,第三期工程承包權的概率分別是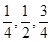 .記“甲乙至少獲得1期工程”為事件
.記“甲乙至少獲得1期工程”為事件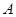 ,甲公司獲得1期工程,乙公司獲得2期工程為事件
,甲公司獲得1期工程,乙公司獲得2期工程為事件 ,甲公司獲得2期工程,乙公司獲得1期工程為事件
,甲公司獲得2期工程,乙公司獲得1期工程為事件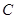 .
.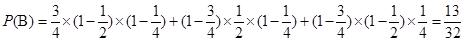 ,
,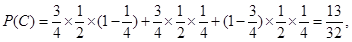
所以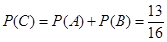
或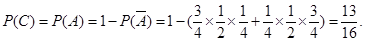
(II)由題意知,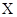 可取
可取 ,
,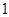 ,
,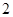 ,
,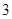 .
.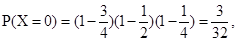
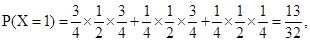
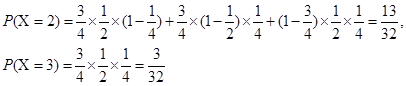
分布列為
所以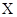

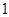
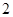
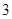

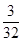
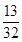
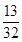
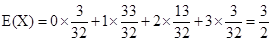 .
.
考點:相互獨立事件同時發生的概率,對立事件的概率,隨機變量的分布列及數學期望.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:解答題
甲、乙兩名同學參加“漢字聽寫大賽”選拔測試,在相同測試條件下,兩人5次測試的成績(單位:分)如下表: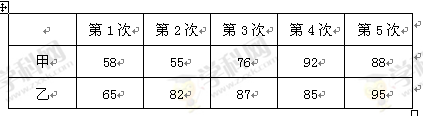
(Ⅰ)請畫出甲、乙兩人成績的莖葉圖. 你認為選派誰參賽更好?說明理由(不用計算);
(Ⅱ)若從甲、乙兩人5次的成績中各隨機抽取一個成績進行分析,設抽到的兩個成績中,90分以上的個數為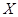 ,求隨機變量
,求隨機變量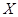 的分布列和期望
的分布列和期望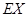 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了參加2013年市級高中籃球比賽,該市的某區決定從四所高中學校選出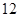 人組成男子籃球隊代表所在區參賽,隊員來源人數如下表:
人組成男子籃球隊代表所在區參賽,隊員來源人數如下表:
| 學校 | 學校甲 | 學校乙 | 學校丙 | 學校丁 |
| 人數 | 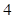 | 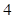 | 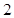 | 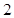 |
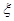 ,求隨機變量
,求隨機變量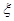 的分布列及數學期望
的分布列及數學期望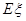 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學校的三個學生社團的人數分布如下表(每名學生只能參加一個社團):
| | 圍棋社 | 舞蹈社 | 拳擊社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
據民生所望,相關部門對所屬服務單位進行整治行核查,規定:從甲類3個指標項中隨機抽取2項,從乙類2個指標項中隨機抽取1項.在所抽查的3個指標項中,3項都優秀的獎勵10萬元;只有甲類2項優秀的獎勵6萬元;甲類只有1項優秀、乙類1項優秀的提出警告,有2項或2項以上不優秀的停業運營并罰款8萬元.已知某家服務單位甲類3項指標項中有2項優秀,乙類2項指標項中有1項優秀.
求:(1)這家單位受到獎勵的概率;
(2)這家單位這次整治性核查中所獲金額的均值(獎勵為正數,罰款為負數).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為貫徹“激情工作,快樂生物”的理念,某單位在工作之余舉行趣味知識有獎競賽,比賽分初賽和決賽兩部分,為了增加節目的趣味性,初賽采用選手選—題答—題的方式進行,每位選手最多有5次選答題的機會,選手累計答對3題或答錯3題即終止其初賽的比賽,答對3題者直接進入決賽,答錯3題者則被淘汰,已知選手甲答題的正確率為 .
.
(1)求選手甲答題次數不超過4次可進入決賽的概率;
(2)設選手甲在初賽中答題的個數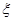 ,試寫出
,試寫出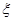 的分布列,并求
的分布列,并求 的數學期望。
的數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
省少年籃球隊要從甲、乙兩所體校選拔隊員。現將這兩所體校共20名學生的身高繪制成如下莖葉圖(單位:cm):若身高在180cm以上(包括180cm)定義為“高個子”,身高在180cm以下(不包括180cm)定義為“非高個子”.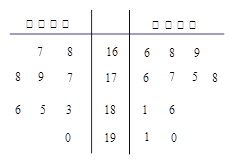
(1)用分層抽樣的方法從“高個子”和“非高個子”中抽取5人,如果從這5人中隨
機選2人,那么至少有一人是“高個子”的概率是多少?
(2)從兩隊的“高個子”中各隨機抽取1人,求恰有1人身高達到190cm的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某居民小區有兩個相互獨立的安全防范系統(簡稱系統)A和B,系統A和B在任意時刻發生故障的概率分別為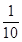 和p.
和p.
(1)若在任意時刻至少有一個系統不發生故障的概率為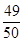 ,求p的值;
,求p的值;
(2)設系統A在3次相互獨立的檢測中不發生故障的次數為隨機變量ξ,求ξ的概率分布列及數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
以下莖葉圖記錄了甲、乙兩組各四名同學的植樹棵數.乙組記錄中有一個數據模糊,無法確認,在圖中以X表示.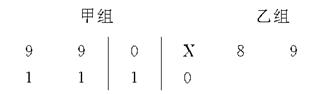
(1)如果X=8,求乙組同學植樹棵數的平均數和方差;
(2)如果X=9,分別從甲、乙兩組中隨機選取一名同學,求這兩名同學的植樹總棵數Y的分布列和數學期望.(注:方差s2=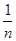 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 為x1,x2,…,xn的平均數)
為x1,x2,…,xn的平均數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com