
(04年廣東卷)(12分)
設函數![]()
(I)證明:當![]() 且
且![]() 時,
時,![]()
(II)點![]() (0<x0<1)在曲線
(0<x0<1)在曲線![]() 上,求曲線上在點
上,求曲線上在點![]() 處的切線與
處的切線與![]() 軸,
軸,![]() 軸正向所圍成的三角形面積的表達式。(用
軸正向所圍成的三角形面積的表達式。(用![]() 表示)
表示)
 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
(05年廣東卷)(14分)
設函數![]() 在
在![]() 上滿足
上滿足![]() ,
,![]() ,且在閉區間[0,7]上,只有
,且在閉區間[0,7]上,只有![]() .
.
(Ⅰ)試判斷函數![]() 的奇偶性;
的奇偶性;
(Ⅱ)試求方程![]() 在閉區間
在閉區間![]() 上的根的個數,并證明你的結論.
上的根的個數,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
(04年廣東卷)(12分)
設函數![]() ,其中常數
,其中常數![]() 為整數
為整數
(I)當![]() 為何值時,
為何值時,![]()
(II)定理:若函數![]() 在
在![]() 上連續,且
上連續,且![]() 與
與![]() 異號,則至少存在一點
異號,則至少存在一點![]() ,使得
,使得![]()
試用上述定理證明:當整數![]() 時,方程
時,方程![]() 在
在![]() 內有兩個實根
內有兩個實根
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高中數學選修1-1 3.3導數在研究函數中的應用練習卷(解析版) 題型:解答題
(2006年廣東卷)設函數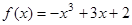 分別在
分別在 、
、 處取得極小值、極大值.
處取得極小值、極大值. 平面上點A、B的坐標分別為
平面上點A、B的坐標分別為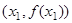 、
、 ,該平面上動點P滿足
,該平面上動點P滿足 ,點Q是點P關于直線
,點Q是點P關于直線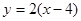 的對稱點
的對稱點
求:(Ⅰ)點A、B的坐標 ;
(Ⅱ)動點Q的軌跡方程
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com