
已知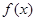 是二次函數,
是二次函數,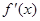 是它的導函數,且對任意的
是它的導函數,且對任意的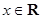 ,
, 恒成立.
恒成立.
(1)求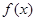 的解析表達式;
的解析表達式;
(2)設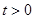 ,曲線
,曲線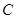 :
: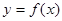 在點
在點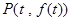 處的切線為
處的切線為 ,
, 與坐標軸圍成的三角形面積為
與坐標軸圍成的三角形面積為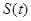 .求
.求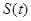 的最小值.
的最小值.
(1) (2)
(2)
【解析】本題主要考查二次函數的概念、導數的應用等知識,以及運算求解能力.在解答過程當中,求導的能力、運算的能力、問題轉換的能力以及數形結合的能力都得到了充分的體現,值得同學們體會反思.
(1)可以現設出二次函數的表達式,結合信息獲得多項式相等進而利用對應系數相等解得參數,即可明確函數解析式;
(2)結合函數的解析式通過求導很容易求的在點P(t,f(t))處的切線l,由此即可表示出三角形的面積關于t的函數S(t).從而利用導函數知識即可求得函數S(t)的最小值
解:(Ⅰ)設 (其中
(其中 ),則
),則 , ………1分
, ………1分
 .
.
由已知,得 ,
,
∴ ,解之,得
,解之,得 ,
, ,
, ,∴
,∴ . ……4分
. ……4分
(2)由(1)得, ,切線
,切線 的斜率
的斜率 ,
,
∴切線 的方程為
的方程為 ,即
,即 . …………6分
. …………6分
從而 與
與 軸的交點為
軸的交點為 ,
, 與
與 軸的交點為
軸的交點為 ,
,
∴ (其中
(其中 ).
………8分
).
………8分
∴ .
……………10分
.
……………10分
當 時,
時, ,
, 是減函數;
是減函數;
當 時,
時, ,
, 是增函數.
……12分
是增函數.
……12分
∴ .
…………13分
.
…………13分


 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:013
[ ]
A.k=0或k=-![]() B.k=0
B.k=0
C.k=-![]() D.k=0或k=
D.k=0或k=![]()
查看答案和解析>>
科目:高中數學 來源:2012屆天津市高三第一次月考理科數學試卷 題型:解答題
已知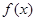 是二次函數,
是二次函數,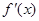 是它的導函數,且對任意的
是它的導函數,且對任意的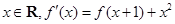 恒成立
恒成立
(Ⅰ)求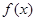 的解析式;
的解析式;
(Ⅱ)設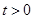 ,曲線
,曲線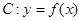 在點
在點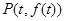 處的切線為
處的切線為 與坐標軸圍成的三角形面積為
與坐標軸圍成的三角形面積為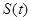 ,求
,求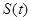 的最小值。
的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
已知![]() 是二次函數,
是二次函數,![]() 是它的導函數,且對任意的
是它的導函數,且對任意的![]() ,
,![]() 恒成立.
恒成立.
(Ⅰ)求![]() 的解析表達式;
的解析表達式;
(Ⅱ)設![]() ,曲線
,曲線![]() :
:![]() 在點
在點![]() 處的切線為
處的切線為![]() ,
,![]() 與坐標軸圍成的三角形面積為
與坐標軸圍成的三角形面積為![]() .求
.求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com