
【題目】設![]() 是實數,
是實數,![]() ,
,
(1)若函數![]() 為奇函數,求
為奇函數,求![]() 的值;
的值;
(2)試用定義證明:對于任意![]() ,
,![]() 在
在![]() 上為單調遞增函數;
上為單調遞增函數;
(3)若函數![]() 為奇函數,且不等式
為奇函數,且不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍。
的取值范圍。
【答案】(1)![]() (2)詳見解析(3)
(2)詳見解析(3)![]()
【解析】
試題分析:(1)函數f(x)為奇函數,故可得f(x)+f(-x)=0,由此方程求m的值;(2)證明于任意m,f(x)在R上為單調函數,由定義法證明即可,設![]() ∈R,
∈R,![]() ,研究
,研究![]() 的符號,根據單調性的定義判斷出結果;(3)因為f(x)在R上為增函數且為奇函數,由此可以將不等式
的符號,根據單調性的定義判斷出結果;(3)因為f(x)在R上為增函數且為奇函數,由此可以將不等式![]() 對任意x∈R恒成立,轉化為
對任意x∈R恒成立,轉化為![]() 即
即![]() 對任意x∈R恒成立,再通過換元進一步轉化為二次不等式恒成立的問題即可解出此時的恒成立的條件
對任意x∈R恒成立,再通過換元進一步轉化為二次不等式恒成立的問題即可解出此時的恒成立的條件
試題解析:(1)∵![]() ,且
,且![]()
∴![]() (注:通過
(注:通過![]() 求也同樣給分)∴
求也同樣給分)∴![]()
(2)證明:設![]() ,則
,則![]()
![]()
![]() ∵
∵![]() ∴
∴![]()
∴![]() 即
即![]() 。 所以
。 所以![]() 在R上為增函數。
在R上為增函數。
(3)因為![]() 為奇函數且在R上為增函數,
為奇函數且在R上為增函數,
由![]() 得:
得: ![]()
∴![]() 即
即![]() 對任意
對任意![]() 恒成立。
恒成立。
令![]()
![]() 問題等價于
問題等價于![]() 對任意
對任意![]() 恒成立。
恒成立。
令![]() ,其對稱軸
,其對稱軸![]()
當![]() 即
即![]() 時,
時,![]() ,符合題意。
,符合題意。
當![]() 時,即
時,即![]() 時,對任意
時,對任意![]() ,
,![]() 恒成立,等價于
恒成立,等價于![]()
解得:![]()
綜上所述,當![]() 時,不等式
時,不等式![]() 對任意
對任意![]() 恒成立
恒成立


科目:高中數學 來源: 題型:
【題目】要產生[-3,3]上的均勻隨機數y,現有[0,1]上的均勻隨機數x,則y可取為( )
A. -3x B. 3x
C. 6x-3 D. -6x-3
查看答案和解析>>
科目:高中數學 來源: 題型:
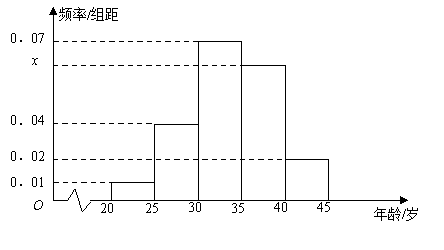
【題目】為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者. 從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是: ![]() .
.
(Ⅰ)求圖中![]() 的值,并根據頻率分布直方圖估計這500名志愿者中年齡在
的值,并根據頻率分布直方圖估計這500名志愿者中年齡在![]() 歲的人數;
歲的人數;
(Ⅱ)在抽出的100名志愿者中按年齡采用分層抽樣的方法抽取10名參加中心廣場的宣傳活動,再從這10名志愿者中選取3名擔任主要負責人. 記這3名志愿者中“年齡低于35歲”的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—1:幾何證明選講
如圖,圓周角∠BAC的平分線與圓交于點D,過點D的切線與弦AC的延長線交于點 E,AD交BC于點F.

(1)求證:BC∥DE;
(2)若D、E、C、F四點共圓,且![]() ,求∠BAC.
,求∠BAC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設定義在![]() 上的函數
上的函數![]() 對于任意實數
對于任意實數![]() ,都有
,都有![]() 成立,且
成立,且![]() ,當
,當![]() 時,
時,![]() .
.
(1)判斷![]() 的單調性,并加以證明;
的單調性,并加以證明;
(2)試問:當![]() 時,
時,![]() 是否有最值?如果有,求出最值;如果沒有,說明理由;
是否有最值?如果有,求出最值;如果沒有,說明理由;
(3)解關于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】重慶一中開展了豐富多彩的社團文化活動,甲,乙,丙三位同學在被問到是否參加過街舞社,動漫社,器樂社這三個社團時,
甲說:我參加過的社團比乙多,但沒有參加過動漫社;
乙說:我沒有參加過器樂社;
丙說:我們三個人都參加過同一個社團,由此判斷乙參加過的社團為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com