
【題目】已知函數f(x)= ![]() sin2x﹣cos2x.
sin2x﹣cos2x.
(1)求函數f(x)的最小正周期和最大值;
(2)求函數f(x)的單調遞減區間.
【答案】
(1)解:f(x)=2( ![]() sin2x﹣
sin2x﹣ ![]() cos2x)=2sin(2x﹣
cos2x)=2sin(2x﹣ ![]() ),
),
∵ω=2,∴T= ![]() =π;
=π;
∵﹣1≤sin(2x﹣ ![]() )≤1,即﹣2≤2sin(2x﹣
)≤1,即﹣2≤2sin(2x﹣ ![]() )≤2,
)≤2,
則f(x)的最大值為2
(2)解:令 ![]() +2kπ≤2x﹣
+2kπ≤2x﹣ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得: ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
則函數f(x)的單調遞減區間為[ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
【解析】(1)函數解析式提取2變形后,利用兩角和與差的正弦函數公式化為一個角的正弦函數,找出ω的值,代入周期公式即可求出最小正周期;根據正弦函數的值域即可確定出f(x)的最大值;(2)根據正弦函數的單調性即可確定出f(x)的遞減區間.
【考點精析】關于本題考查的兩角和與差的正弦公式和正弦函數的單調性,需要了解兩角和與差的正弦公式:![]() ;正弦函數的單調性:在
;正弦函數的單調性:在![]()
![]() 上是增函數;在
上是增函數;在![]()
![]() 上是減函數才能得出正確答案.
上是減函數才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC內的一點.
,AC=3, BC=2,P是△ABC內的一點.
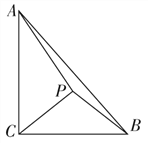
(1)若P是等腰直角三角形PBC的直角頂點,求PA的長;
(2)若∠BPC=![]() ,設∠PCB=θ,求△PBC的面積S(θ)的解析式,并求S(θ)的最大值.
,設∠PCB=θ,求△PBC的面積S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是定義在R上的奇函數,當x≥0時,f(x)=2x﹣x2 .
(1)求x<0時f(x)的解析式;
(2)問是否存在正數a,b,當x∈[a,b]時,g(x)=f(x),且g(x)的值域為[ ![]() ,
, ![]() ]?若存在,求出所有的a,b的值,若不存在,請說明理由.
]?若存在,求出所有的a,b的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年3月9日至15日,谷歌人工智能系統“阿爾法”迎戰圍棋冠軍李世石,最終結果“阿爾法”以總比分4比1戰勝李世石.許多人認為這場比賽是人類的勝利,也有許多人持反對意見,有網友為此進行了調查,在參加調查的2548名男性中有1560名持反對意見,2452名女性中有1200名持反對意見,在運用這些數據說明“性別”對判斷“人機大戰是人類的勝利”是否有關系時,應采用的統計方法是( )
A.莖葉圖
B.分層抽樣
C.獨立性檢驗
D.回歸直線方程
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)選修4—4:坐標系與參數方程
在直角坐標系xOy中,圓C的參數方程![]() 為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(1)求圓C的極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() 與圓C的交點為O、P,與直線
與圓C的交點為O、P,與直線![]() 的交點為Q,求線段PQ的長.
的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】Sn表示等差數列{an}的前n項的和,且S4=S9 , a1=﹣12
(1)求數列的通項an及Sn;
(2)求和Tn=|a1|+|a2|+…+|an|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com