
���}Ŀ����֪����(sh��)![]()
��1��������![]() ���c(di��n)
���c(di��n)![]() ̎���о��cֱ��
̎���о��cֱ��![]() ��ֱ����(sh��)�ĘOֵ��
��ֱ����(sh��)�ĘOֵ��
��2���O(sh��)����(sh��)![]() .��(d��ng)
.��(d��ng)![]() =
=![]() �r(sh��)����^(q��)�g[1��e]�ϴ���x0��ʹ��
�r(sh��)����^(q��)�g[1��e]�ϴ���x0��ʹ��![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ��������
��ȡֵ��������![]() ����Ȼ��(du��)��(sh��)�ה�(sh��)��
����Ȼ��(du��)��(sh��)�ה�(sh��)��
���𰸡���1���OСֵ��![]() ����2��
����2��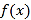
��������ԇ�}��������1���������(sh��)�Č�(d��o)��(sh��)��Ӌ(j��)��![]() ��ֵ�����
��ֵ�����![]() ���Ķ����
���Ķ����![]() �Ć��{(di��o)�^(q��)�g���������(sh��)�ĘOֵ���ɣ���2����
�Ć��{(di��o)�^(q��)�g���������(sh��)�ĘOֵ���ɣ���2����![]() ������(j��)����(sh��)�Ć��{(di��o)�����
������(j��)����(sh��)�Ć��{(di��o)�����![]() ����Сֵ���Ķ����
����Сֵ���Ķ����![]() �ķ�������.
�ķ�������.
ԇ�}��������1��![]() ��
��![]() ������?y��n)�����
������?y��n)�����![]() ���c(di��n)��1��f��1����̎���о��cֱ��
���c(di��n)��1��f��1����̎���о��cֱ��![]() ��ֱ������
��ֱ������![]() ����
����![]() �����
�����![]() ������
������![]() �� �ஔ(d��ng)
�� �ஔ(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ��
�� ![]() ��
��![]() �φ��{(di��o)�f�p����(d��ng)
�φ��{(di��o)�f�p����(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ��f��x������2��+�����φ��{(di��o)�f�����ஔ(d��ng)x=2�r(sh��)��f��x��ȡ�ØOСֵ
��f��x������2��+�����φ��{(di��o)�f�����ஔ(d��ng)x=2�r(sh��)��f��x��ȡ�ØOСֵ![]() ����f��x���OСֵ��ln2��
����f��x���OСֵ��ln2��
��2����![]() ���t
���t![]() ����ʹ�څ^(q��)�g��
����ʹ�څ^(q��)�g��![]() �ϴ���
�ϴ���![]() ��ʹ��
��ʹ��![]() ��ֻ���څ^(q��)�g
��ֻ���څ^(q��)�g![]() ��
��![]() ����СֵС���㣮��
����СֵС���㣮��![]() �ã�
�ã� ![]() ��
��![]() ����(d��ng)
����(d��ng)![]() ����
����![]() �r(sh��)��
�r(sh��)�� ![]() ��
��![]() �φ��{(di��o)�f�p���t
�φ��{(di��o)�f�p���t![]() ����Сֵ��
����Сֵ��![]() ����
����![]() �����
�����![]() ����
����![]() ����
����![]() ����(d��ng)
����(d��ng)![]() ����
����![]() �r(sh��)��
�r(sh��)�� ![]() ��
��![]() �φ��{(di��o)�f�����t
�φ��{(di��o)�f�����t![]() ����Сֵ��
����Сֵ��![]() ����
����![]() �����
�����![]() ����
����![]() ����(d��ng)
����(d��ng)![]() ����
����![]() �r(sh��)��
�r(sh��)�� ![]() ��
��![]() �φ��{(di��o)�f�p����
�φ��{(di��o)�f�p����![]() �φ��{(di��o)�f�����t
�φ��{(di��o)�f�����t![]() ����Сֵ��
����Сֵ��![]() ����
����![]() ����
����![]() ����
����![]() ���˕r(sh��)
���˕r(sh��)![]() ���������C����������(sh��)��(sh��)m��ȡֵ������
���������C����������(sh��)��(sh��)m��ȡֵ������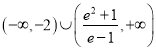



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��������(sh��)![]() �ĈD���ϴ��ڃɂ�(g��)��ͬ���c(di��n)
�ĈD���ϴ��ڃɂ�(g��)��ͬ���c(di��n)![]() ��
��![]() ��ʹ������
��ʹ������![]() ���@���c(di��n)̎���о��غϣ��Q����(sh��)
���@���c(di��n)̎���о��غϣ��Q����(sh��)![]() ����
����![]() ���|(zh��).�����(sh��)���
���|(zh��).�����(sh��)���![]() ���|(zh��)���� ��
���|(zh��)���� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������¼�A,B�Ǫ�(d��)���¼�����(����)
A. һöӲ�ŔS�ɴ�,A=����һ�Ξ��������ϡ�,B=���ڶ��Ξ鷴�����ϡ�
B. �����Ѓɂ�(g��)����̓ɂ�(g��)����,���Żص�������,A=����һ����������,B=���ڶ�����������
C. �Sһö����,A=�����F(xi��n)�c(di��n)��(sh��)���攵(sh��)��,B=�����F(xi��n)�c(di��n)��(sh��)��ż��(sh��)��
D. A=�����ܻ20�q��,B=�����ܻ50�q��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�������(bi��o)ԭ�c(di��n)
�У�������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)����
��O�c(di��n)����![]() �S�����S��O�S�����O����(bi��o)ϵ����֪����
�S�����S��O�S�����O����(bi��o)ϵ����֪����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1��������![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2����ɗl���ഹֱ��ֱ������(j��ng)�^(gu��)ԭ�c(di��n)���ɗlֱ���c����(bi��o)�S�����غϣ����c����![]() �քe�����c(di��n)
�քe�����c(di��n)![]() ������ԭ�c(di��n)������
������ԭ�c(di��n)������![]() �����@�ɗlֱ����ֱ������(bi��o)����.
�����@�ɗlֱ����ֱ������(bi��o)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵxOy�У���ֱ֪��l�^(gu��)�c(di��n)P��2��2��.������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ������C�ĘO����(bi��o)���̞�������cos2����4cos����0.
��1����C��ֱ������(bi��o)���̣�
��2����l�cC����A��B���c(di��n)���� �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)��(sh��)��![]() ǰ
ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() ,��(du��)����
,��(du��)����![]() ,�c(di��n)
,�c(di��n)![]() ���ں���(sh��)
���ں���(sh��)![]() �D���ϣ�
�D���ϣ�
��1����![]() ��
��![]() ��
��![]() ,�����딵(sh��)��
,�����딵(sh��)��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2���Ô�(sh��)�W(xu��)�w�{���C����1���IJ��룻
��3������(sh��)��![]() �M�㣺
�M�㣺![]() ,
,![]() ,�Ҍ�(du��)�����
,�Ҍ�(du��)�����![]() ,����
,����![]() ��
��![]() ��
��![]() �ɹ��Ȟ�
�ɹ��Ȟ�![]() �ĵȱȔ�(sh��)��,
�ĵȱȔ�(sh��)��,![]() ��
��![]() ��
��![]() �ɵȲ(sh��)��,�O(sh��)
�ɵȲ(sh��)��,�O(sh��)![]() ,��(sh��)��
,��(sh��)��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2��������(sh��)![]() ��
��![]() �ϟo(w��)���c(di��n)����
�ϟo(w��)���c(di��n)����![]() ��Сֵ.
��Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һ�����������(j��)����ij�N������N��ӛ䛣��L�������N�������l�ʷֲ�ֱ���D����D231��ʾ��
 �D231
�D231
�����N����������M���l��ҕ����ʣ������O(sh��)ÿ����N�������(d��)����
(1)����δ��(l��i)�B�m(x��)3������B�m(x��)2������N������������100��(g��)����1������N��������50��(g��)�ĸ��ʣ�
(2)��X��ʾ��δ��(l��i)3�������N����������100��(g��)���씵(sh��)�����S�C(j��)׃��X�ķֲ��У�����E(X)������D(X)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������С�}�M��10�֣��x��4��4������(bi��o)ϵ�c����(sh��)����
��֪����![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() �酢��(sh��)��.
�酢��(sh��)��.
��I����������![]() �ą���(sh��)���̣�ֱ��
�ą���(sh��)���̣�ֱ��![]() ����ͨ���̣�
����ͨ���̣�
��II���^(gu��)����![]() ������һ�c(di��n)
������һ�c(di��n)![]() ���c
���c![]() �A�Ǟ�
�A�Ǟ�![]() ��ֱ������
��ֱ������![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �����ֵ�c��Сֵ��
�����ֵ�c��Сֵ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com