
若定義在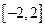 上的奇函數
上的奇函數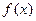 滿足當
滿足當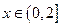 時,
時,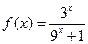 .
.
(1)求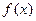 在
在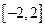 上的解析式;
上的解析式;
(2)判斷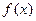 在
在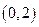 上的單調性,并給予證明;
上的單調性,并給予證明;
(3)當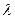 為何值時,關于方程
為何值時,關于方程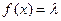 在
在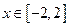 上有實數解?
上有實數解?
 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分13 分) 2010年11月在廣州召開亞
分) 2010年11月在廣州召開亞 運會,某小商品公司開發一種亞運會紀念品,每件產品的成本是15元,銷售價是20元,月平
運會,某小商品公司開發一種亞運會紀念品,每件產品的成本是15元,銷售價是20元,月平 均銷售a件,通過改進工藝,產品的成本不變,質量和技術含金量提高,市場分析的結果表明:如果產品的銷售價提高的百分率為x(0<x<1),那么月平均
均銷售a件,通過改進工藝,產品的成本不變,質量和技術含金量提高,市場分析的結果表明:如果產品的銷售價提高的百分率為x(0<x<1),那么月平均 銷售量減少的百分率為x2,記改進工藝后,該公司銷售紀念品的月平均利潤是y(元).
銷售量減少的百分率為x2,記改進工藝后,該公司銷售紀念品的月平均利潤是y(元).
(1)寫出y與x的函數關系式;
(2)改進工藝后,確定該紀念品的售價,使該公司銷售該紀念品的月平均利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)設二次函數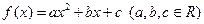 滿足下列條件:
滿足下列條件:
①當 ∈R時,
∈R時, 的最小值為0,且f (
的最小值為0,且f ( -1)=f(-
-1)=f(- -1)成立;
-1)成立;
②當 ∈(0,5)時,
∈(0,5)時, ≤
≤ ≤2
≤2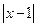 +1恒成立。
+1恒成立。
(1)求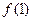 的值;
的值;
(2)求 的解析式;
的解析式;
(3)求最大的實數m(m>1),使得存在實數t,只要當 ∈
∈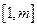 時,就有
時,就有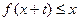 成立。
成立。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com