
【題目】已知函數 ![]()
(1)函數 ![]() 在
在 ![]() 上有兩個不同的零點,求
上有兩個不同的零點,求 ![]() 的取值范圍;
的取值范圍;
(2)當 ![]() 時,
時, ![]() 的最大值為
的最大值為 ![]() ,求
,求 ![]() 的最小值;
的最小值;
(3)函數 ![]() ,對于任意
,對于任意 ![]() 存在
存在 ![]() ,使得
,使得 ![]() ,試求
,試求 ![]() 的取值范圍.
的取值范圍.
【答案】
(1)解: ![]()
![]()
![]()
![]()
令 ![]()
則 ![]() 在
在 ![]() 上有兩個不同實根
上有兩個不同實根
于是, 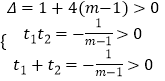
解得 ![]()
(2)解: ![]()
![]()
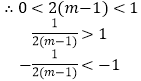
![]()
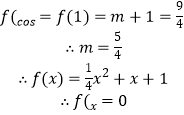
(3)解:由題意可知: ![]()
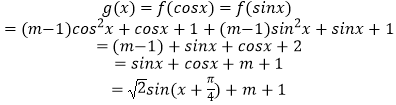
由題意 ![]() 有解
有解
當 ![]() 時,不等式不成立
時,不等式不成立
當 ![]() 時,
時, ![]()
令 ![]() ,
, ![]()

綜上,m的取值范圍為 ![]()
【解析】(1)通過換元法以及二次函數的性質求出m的范圍即可。(2)求出f(cosx)的解析式根據函數的單調性求出函數的最大值,得到關于m的方程即可求出m的值從而求出函數的解析式故可得到函數的最小值。(3)把問題轉化為 g(x) min![]() f(t) 有解求出 g(x) 的最小值,再分離參數m利用函數的單調性求出m的范圍即可。
f(t) 有解求出 g(x) 的最小值,再分離參數m利用函數的單調性求出m的范圍即可。
【考點精析】根據題目的已知條件,利用函數單調性的性質和二次函數的性質的相關知識可以得到問題的答案,需要掌握函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:
【題目】在如圖的程序框圖表示的算法中,輸入三個實數a,b,c,要求輸出的x是這三個數中最大的數,那么在空白的判斷框中,應該填入( ) 
A.x>c
B.c>x
C.c>b
D.c>a
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點(1, ![]() )是函數f(x)=
)是函數f(x)= ![]() ax(a>0,a≠1)圖象上一點,等比數列{an}的前n項和為c﹣f(n).數列{bn}(bn>0)的首項為2c,前n項和滿足
ax(a>0,a≠1)圖象上一點,等比數列{an}的前n項和為c﹣f(n).數列{bn}(bn>0)的首項為2c,前n項和滿足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求數列{an}的通項公式;
+1(n≥2). (Ⅰ)求數列{an}的通項公式;
(Ⅱ)若數列{ ![]() }的前n項和為Tn , 問使Tn>
}的前n項和為Tn , 問使Tn> ![]() 的最小正整數n是多少?
的最小正整數n是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】葫蘆島市某工廠黨委為了研究手機對年輕職工工作和生活的影響情況做了一項調查:在廠內用簡單隨機抽樣方法抽取了30名25歲至35歲的職工,對其“每十天累計看手機時間”(單位:小時)進行調查,得到莖葉圖如下.所抽取的男職工“每十天累計看手機時間”的平均值和所抽取的女生 “每十天累計看手機時間”的中位數分別是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C所對的邊分別為a,b,c,已知向量 ![]() ,
, ![]() ,且
,且 ![]() .
.
(1)求角B的大小;
(2)若b=2,△ABC的面積為 ![]() ,求a+c的值.
,求a+c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱ABCD﹣A1B1C1D1中,側面A1ADD1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點.
,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點. 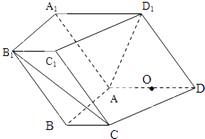
(1)求證:A1O∥平面AB1C;
(2)求銳二面角A﹣C1D1﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐 ![]() 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形, ![]() ,
, ![]() ,平面
,平面 ![]() 底面ABCD, O為AD的中點, M是棱PC上的點, AD=2AB.
底面ABCD, O為AD的中點, M是棱PC上的點, AD=2AB.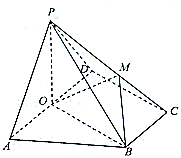
(1)求證:平面 ![]() 平面PAD;
平面PAD;
(2)若 ![]() 平面BMO,求
平面BMO,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,傾斜角為 ![]() 的直線l與曲線C:
的直線l與曲線C: ![]() ,(α為參數)交于A,B兩點,且|AB|=2,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,則直線l的極坐標方程是 .
,(α為參數)交于A,B兩點,且|AB|=2,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,則直線l的極坐標方程是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P(x,y)在圓x2+y2﹣6x﹣6y+14=0上
(1)求 ![]() 的最大值和最小值;
的最大值和最小值;
(2)求x2+y2+2x+3的最大值與最小值;
(3)求x+y的最大值與最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com