
下列命題:
①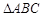 中,若
中,若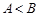 ,則
,則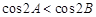 ;
;
②若A,B,C為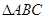 的三個內角,則
的三個內角,則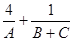 的最小值為
的最小值為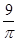
③已知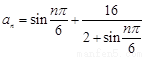
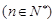 ,則數列
,則數列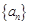 中的最小項為
中的最小項為 ;
;
④若函數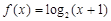 ,且
,且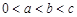 ,則
,則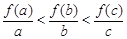 ;
;
⑤函數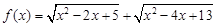 的最小值為
的最小值為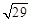 .
.
其中所有正確命題的序號是
②③
【解析】
試題分析:①△ABC中,若A<B,則a<b,由正弦定理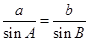
得0<sinA<sinB,又cos2A=1-2sin2A,cos2B=1-2sin2B,
所以cos2A>cos2B,①錯誤.
②因為A+B+C=π,α=A,β=B+C,α+β=π
所以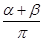 =1,
=1,
原式等價于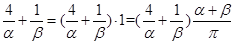
=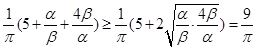 ,
,
當且僅當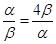 ,即α=2β時取等號.所以②正確.
,即α=2β時取等號.所以②正確.
③因為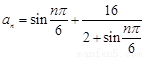 =2+
=2+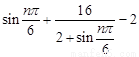 ,因為1≤
,因為1≤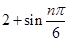 ≤3,
≤3,
所以設t=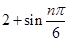 ,則1≤t≤3.因為函數y=t+
,則1≤t≤3.因為函數y=t+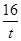 -2在區間(0,4)上單調遞減,所以在[1,3]上單調遞減,因此,當t=3時,函數有最小值3+
-2在區間(0,4)上單調遞減,所以在[1,3]上單調遞減,因此,當t=3時,函數有最小值3+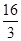 -2=
-2=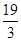 ,則對應數列{an}中的最小項為
,則對應數列{an}中的最小項為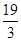 ,所以③正確.
,所以③正確.
④令g(x)=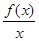 ,則函數g(x)的幾何意義為曲線上點與原點連線斜率的大小.由題意可知
,則函數g(x)的幾何意義為曲線上點與原點連線斜率的大小.由題意可知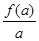 ,
,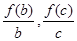 分別看作函數f(x)=log2(x+1)圖象上的點(a,f(a)),(b,f(b)),(c,f(b))與原點連線的斜率,由圖象可知,
分別看作函數f(x)=log2(x+1)圖象上的點(a,f(a)),(b,f(b)),(c,f(b))與原點連線的斜率,由圖象可知,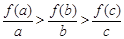 ,所以④錯誤.
,所以④錯誤.
⑤因為,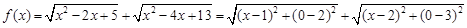 ,問題轉化成點P(x,0)到A(1,2),B(2,3)距離之和的最小值。原式等價為|PA|+|PB|的最小值,找出點A關于x軸的對稱點D(1,-2).
,問題轉化成點P(x,0)到A(1,2),B(2,3)距離之和的最小值。原式等價為|PA|+|PB|的最小值,找出點A關于x軸的對稱點D(1,-2).
則|PA|+|PB|=|PD|+|PB|≥|PD|,所以最小值為|PD|=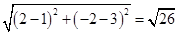 .
.
所以,⑤錯誤.故答案為:②③.
考點:正弦定理的應用,均值定理的應用,對號函數的性質,對數函數的圖象和性質。
點評:難題,本題綜合性較強,難度較大。靈活的對問題實施轉化,是解題的關鍵。


科目:高中數學 來源: 題型:
| 4 |
| A |
| 1 |
| B+C |
| 9 |
| π |
| nπ |
| 6 |
| 16 | ||
2+sin
|
| 19 |
| 3 |
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
| x2-2x+5 |
| x2-4x+13 |
| 29 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省聊城市高三下學期期初考試文科數學試卷(解析版) 題型:選擇題
下列命題:①在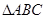 中,若
中,若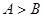 ,則
,則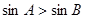 ;②已知
;②已知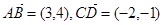 ,則
,則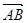 在
在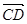 上的投影為
上的投影為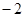 ;③已知
;③已知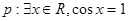 ,
,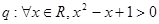 ,則“
,則“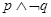 ”為假命題.其中真命題的個數為( )
”為假命題.其中真命題的個數為( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省聊城市高三下學期期初考試文科數學試卷(解析版) 題型:選擇題
下列命題:①在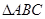 中,若
中,若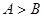 ,則
,則 ;②已知
;②已知 ,則
,則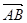 在
在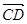 上的投影為
上的投影為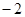 ;③已知
;③已知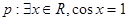 ,
,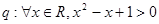 ,則“
,則“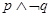 ”為假命題.其中真命題的個數為( )
”為假命題.其中真命題的個數為( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源:2014屆四川省成都外國語學校高一下學期期中數學試卷(解析版) 題型:填空題
對于下列命題:①在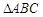 中,若
中,若 ,則
,則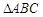 一定是銳角三角形;
一定是銳角三角形;
②在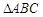 中,
中,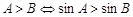 ;③若數列
;③若數列 是等比數列,則數列
是等比數列,則數列 也是等比數列;
也是等比數列;
④若 ,則
,則 的最小值是
的最小值是 .以上正確的命題的序號是_________
.以上正確的命題的序號是_________
查看答案和解析>>
科目:高中數學 來源:2010年江西省高一第四次月考數學卷 題型:填空題
下列命題:①△ABC中,若A>B,則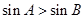 ;②若對一切
;②若對一切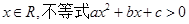 恒成立,則必有
恒成立,則必有 ;③不等式
;③不等式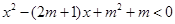 的解集為
的解集為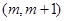 ;④函數
;④函數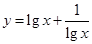 最小值為2,其中正確的序號為__________ 。
最小值為2,其中正確的序號為__________ 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com