
【題目】某企業(yè)打算處理一批產(chǎn)品,這些產(chǎn)品每箱100件,以箱為單位銷售.已知這批產(chǎn)品中每箱出現(xiàn)的廢品率只有![]() 或者
或者![]() 兩種可能,兩種可能對(duì)應(yīng)的概率均為0.5.假設(shè)該產(chǎn)品正品每件市場(chǎng)價(jià)格為100元,廢品不值錢.現(xiàn)處理價(jià)格為每箱8400元,遇到廢品不予更換.以一箱產(chǎn)品中正品的價(jià)格期望值作為決策依據(jù).
兩種可能,兩種可能對(duì)應(yīng)的概率均為0.5.假設(shè)該產(chǎn)品正品每件市場(chǎng)價(jià)格為100元,廢品不值錢.現(xiàn)處理價(jià)格為每箱8400元,遇到廢品不予更換.以一箱產(chǎn)品中正品的價(jià)格期望值作為決策依據(jù).
(1)在不開箱檢驗(yàn)的情況下,判斷是否可以購(gòu)買;
(2)現(xiàn)允許開箱,有放回地隨機(jī)從一箱中抽取2件產(chǎn)品進(jìn)行檢驗(yàn).
①若此箱出現(xiàn)的廢品率為![]() ,記抽到的廢品數(shù)為
,記抽到的廢品數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
②若已發(fā)現(xiàn)在抽取檢驗(yàn)的2件產(chǎn)品中,其中恰有一件是廢品,判斷是否可以購(gòu)買.
【答案】(1) 在不開箱檢驗(yàn)的情況下,可以購(gòu)買. (2) ①分布列見解析,0.4 ②不可以購(gòu)買
【解析】
(1)求出在不開箱檢驗(yàn)的情況下,一箱產(chǎn)品中正品的價(jià)格期望值,即得解;(2)①![]() 的可能取值為0,1,2,再求出對(duì)應(yīng)的概率,即得
的可能取值為0,1,2,再求出對(duì)應(yīng)的概率,即得![]() 的分布列和數(shù)學(xué)期望;②一箱產(chǎn)品中,設(shè)正品的價(jià)格的期望值為
的分布列和數(shù)學(xué)期望;②一箱產(chǎn)品中,設(shè)正品的價(jià)格的期望值為![]() ,求出
,求出![]() 即得解.
即得解.
(1)在不開箱檢驗(yàn)的情況下,一箱產(chǎn)品中正品的價(jià)格期望值為:
![]() ,
,
∴在不開箱檢驗(yàn)的情況下,可以購(gòu)買.
(2)①![]() 的可能取值為0,1,2,
的可能取值為0,1,2,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 |
| 0.64 | 0.32 | 0.04 |
![]() .
.
②設(shè)事件![]() :發(fā)現(xiàn)在抽取檢驗(yàn)的2件產(chǎn)品中,其中恰有一件是廢品,
:發(fā)現(xiàn)在抽取檢驗(yàn)的2件產(chǎn)品中,其中恰有一件是廢品,
則![]() ,
,
一箱產(chǎn)品中,設(shè)正品的價(jià)格的期望值為![]() ,則
,則![]() ,
,
事件![]()
![]() 的一箱,
的一箱,
則![]() ,
,
事件![]() :抽取的廢品率為
:抽取的廢品率為![]() 的一箱,
的一箱,
則![]() ,
,
∴![]() ,
,
∴已發(fā)現(xiàn)在抽取檢驗(yàn)的2件產(chǎn)品中,其中恰有一件是廢品,不可以購(gòu)買.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱錐![]() 中,
中,![]() 是等邊三角形,
是等邊三角形,![]() 是線段
是線段![]() 的中點(diǎn),
的中點(diǎn),![]() 是線段
是線段![]() 上靠近
上靠近![]() 的四等分點(diǎn),平面
的四等分點(diǎn),平面![]() 平面
平面![]() .
.
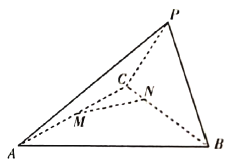
(1)求證:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年6月25日,《固體廢物污染環(huán)境防治法(修訂草案)》初次提請(qǐng)全國(guó)人大常委會(huì)審議,草案對(duì)“生活垃圾污染環(huán)境的防治”進(jìn)行了專章規(guī)定.草案提出,國(guó)家推行生活垃圾分類制度.為了了解人民群眾對(duì)垃圾分類的認(rèn)識(shí),某市環(huán)保部門對(duì)該市市民進(jìn)行了一次垃圾分類網(wǎng)絡(luò)知識(shí)問卷調(diào)查,每一位市民僅有一次參加機(jī)會(huì),通過隨機(jī)抽樣,得到參加問卷調(diào)查的1000人的得分(滿分:100分)數(shù)據(jù),統(tǒng)計(jì)結(jié)果如表所示:
得分 |
|
|
|
|
|
|
|
頻數(shù) | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由頻數(shù)分布表可以認(rèn)為,此次問卷調(diào)查的得分![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作為代表),請(qǐng)利用正態(tài)分布的知識(shí)求
近似為這1000人得分的平均值(同一組數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作為代表),請(qǐng)利用正態(tài)分布的知識(shí)求![]() ;
;
(2)在(1)的條件下,市環(huán)保部門為此次參加問卷調(diào)查的市民制定如下獎(jiǎng)勵(lì)方案:
①得分不低于![]() “的可以獲贈(zèng)2次隨機(jī)話費(fèi),得分低于
“的可以獲贈(zèng)2次隨機(jī)話費(fèi),得分低于![]() 的可以獲贈(zèng)1次隨機(jī)話費(fèi);
的可以獲贈(zèng)1次隨機(jī)話費(fèi);
②每次獲贈(zèng)的隨機(jī)話費(fèi)和對(duì)應(yīng)的概率為:
獲贈(zèng)的隨機(jī)話費(fèi)(單位:元) | 20 | 40 |
概率 |
|
|
現(xiàn)市民小王要參加此次問卷調(diào)查,記![]() (單位:元)為該市民參加問卷調(diào)查獲贈(zèng)的話費(fèi),求
(單位:元)為該市民參加問卷調(diào)查獲贈(zèng)的話費(fèi),求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
附:①![]() ;②若
;②若![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)![]() 年的純利潤(rùn)為
年的純利潤(rùn)為![]() 萬元,因設(shè)備老化等原因,企業(yè)的生產(chǎn)能力將逐年下降,若不進(jìn)行技術(shù)改造,預(yù)測(cè)從今年(
萬元,因設(shè)備老化等原因,企業(yè)的生產(chǎn)能力將逐年下降,若不進(jìn)行技術(shù)改造,預(yù)測(cè)從今年(![]() 年)起每年比上一年純利潤(rùn)減少
年)起每年比上一年純利潤(rùn)減少![]() 萬元,今年初該企業(yè)一次性投入資金
萬元,今年初該企業(yè)一次性投入資金![]() 萬元進(jìn)行技術(shù)改造,預(yù)計(jì)在未扣除技術(shù)改造資金的情況下,第
萬元進(jìn)行技術(shù)改造,預(yù)計(jì)在未扣除技術(shù)改造資金的情況下,第![]() 年(今年為第一年)的利潤(rùn)為
年(今年為第一年)的利潤(rùn)為![]() 萬元(
萬元(![]() 為正整數(shù)).
為正整數(shù)).
(1)設(shè)從今年起的前![]() 年,若該企業(yè)不進(jìn)行技術(shù)改造的累計(jì)純利潤(rùn)為
年,若該企業(yè)不進(jìn)行技術(shù)改造的累計(jì)純利潤(rùn)為![]() 萬元,進(jìn)行技術(shù)改造后的累計(jì)純利潤(rùn)為
萬元,進(jìn)行技術(shù)改造后的累計(jì)純利潤(rùn)為![]() 萬元(須扣除技術(shù)改造資金),求
萬元(須扣除技術(shù)改造資金),求![]() ,
,![]() 的表達(dá)式;
的表達(dá)式;
(2)以上述預(yù)測(cè),從今年起該企業(yè)至少經(jīng)過多少年后,進(jìn)行技術(shù)改造后的累計(jì)純利潤(rùn)超過不進(jìn)行技術(shù)改造的累計(jì)純利潤(rùn)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】空氣質(zhì)量指數(shù)![]() 是反映空氣質(zhì)量狀況的指數(shù),
是反映空氣質(zhì)量狀況的指數(shù),![]() 指數(shù)值越小,表明空氣質(zhì)量越好,其對(duì)應(yīng)關(guān)系如表:
指數(shù)值越小,表明空氣質(zhì)量越好,其對(duì)應(yīng)關(guān)系如表:
|
|
|
|
|
|
|
空氣質(zhì)量 | 優(yōu) | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴(yán)重污染 |
如圖是某市10月1日—20日![]() 指數(shù)變化趨勢(shì):
指數(shù)變化趨勢(shì):
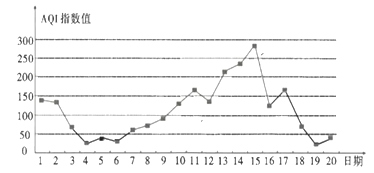
下列敘述正確的是( )
A.該市10月的前半個(gè)月的空氣質(zhì)量越來越好
B.這20天中的中度污染及以上的天數(shù)占![]()
C.這20天中![]() 指數(shù)值的中位數(shù)略高于100
指數(shù)值的中位數(shù)略高于100
D.總體來說,該市10月上旬的空氣質(zhì)量比中旬的空氣質(zhì)量差
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,已知![]() ,頂點(diǎn)P在平面ABC上的射影為
,頂點(diǎn)P在平面ABC上的射影為![]() 的外接圓圓心.
的外接圓圓心.
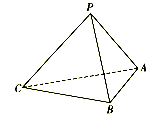
(1)證明:平面![]() 平面ABC;
平面ABC;
(2)若點(diǎn)M在棱PA上,![]() ,且二面角P-BC-M的余弦值為
,且二面角P-BC-M的余弦值為![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過![]() 軸上動(dòng)點(diǎn)
軸上動(dòng)點(diǎn)![]() 引拋物線
引拋物線![]() 的兩條切線
的兩條切線![]() ,
,![]() ,其中
,其中![]() ,
,![]() 為切線.
為切線.
(1)若切線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() 和
和![]() ,求證:
,求證:![]() 為定值,并求出定值;
為定值,并求出定值;
(2)當(dāng)![]() 最小時(shí),求
最小時(shí),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知 m、n 是兩條不同的直線,α、β、γ是三個(gè)不同的平面,下列命題中正確的是( )
A.若α⊥β , β⊥γ ,則α∥γ
B.若 ![]() ,
, ![]() , m∥n ,則α∥β
, m∥n ,則α∥β
C.若 m、n 是異面直線, ![]() , m∥β ,
, m∥β , ![]() , n∥α ,則α∥β
, n∥α ,則α∥β
D.平面α內(nèi)有不共線的三點(diǎn)到平面 β的距離相等,則α∥β
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“干支紀(jì)年法”是中國(guó)歷法上自古以來就一直使用的紀(jì)年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被稱為“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字開始,“地支”以“子”字開始,兩者按照干支順序相配,構(gòu)成了“干支紀(jì)年法”,其相配順序?yàn)椋杭鬃印⒁页蟆⒈?/span>![]() 癸酉、甲戌、乙亥、丙子
癸酉、甲戌、乙亥、丙子![]() 癸未、甲申、乙酉、丙戌
癸未、甲申、乙酉、丙戌![]() 癸巳
癸巳![]() 癸亥,60為一個(gè)周期,周而復(fù)始,循環(huán)記錄.按照“干支紀(jì)年法”,中華人民共和國(guó)成立的那年為己丑年,則2013年為( )
癸亥,60為一個(gè)周期,周而復(fù)始,循環(huán)記錄.按照“干支紀(jì)年法”,中華人民共和國(guó)成立的那年為己丑年,則2013年為( )
A.甲巳年B.壬辰年C.癸巳年D.辛卯年
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com