【題目】（本小題滿分12分）橢圓
（
）的上頂點為
， 
是
上的一點，以
為直徑的圓經過橢圓
的右焦點
．
（1）求橢圓
的方程；
（2）動直線
與橢圓
有且只有一個公共點，問：在
軸上是否存在兩個定點，它們到直線
的距離之積等于
？如果存在，求出這兩個定點的坐標；如果不存在，說明理由．
【答案】（1）
；（2）存在兩個定點
， 
．
【解析】試題（1）設
．以
為直徑的圓經過橢圓
的右焦點
即
，從而得到b,c的一個方程，然后將點P代入橢圓方程得到a,b的一個方程，再結合
,三個量三個方程，從而求出參數a,b，進而求出橢圓方程；（2）是否存在性問題應假設存在去求解．當直線
的斜率存在時，設其方程為
，由其與橢圓有且只有一個公共點得到
．假設存在兩點
， 
滿足題設，然后得到
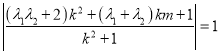．因與參數k,m無關，所以令其系數等于零即可求出．
試題解析：（1）
， 
，由題設可知
，得
①
又點
在橢圓
上， 
， 
②
③
①③聯立解得， 
， 
故所求橢圓的方程為
（2）當直線
的斜率存在時，設其方程為
，代入橢圓方程，消去
，
整理得
（
）
方程（
）有且只有一個實根，又
，
所以
，得
假設存在
， 
滿足題設，則由
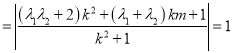對任意的實數
恒成立，
所以， 
解得， 
或
當直線
的斜率不存在時，經檢驗符合題意．
總上，存在兩個定點
， 
，使它們到直線
的距離之積等于
．
同步輕松練習系列答案
課課通課程標準思維方法與能力訓練系列答案科目：高中數學 來源： 題型：
【題目】某工廠加工一批零件，加工過程中會產生次品，根據經驗可知，其次品率p與日產量x（萬件）之間滿足函數關系式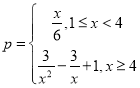
，已知每生產1萬件合格品可獲利2萬元，但生產1萬件次品將虧損1萬元（次品率=次品數/生產量）
（1）試寫出加工這批零件的日盈利額y（萬元）與日產量x（萬件）的函數；
（2）當日產量為多少時，可獲得最大利潤？最大利潤為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某校學生參加社區服務的情況，采用按性別分層抽樣的方法進行調查.已知該校共有學生960人，其中男生560人，從全校學生中抽取了容量為n的樣本，得到一周參加社區服務時間的統計數據如下：
超過1小時 | 不超過1小時 | |
男 | 20 | 8 |
女 | 12 | m |
（1）求m，n；
（2）能否有95%的把握認為該校學生一周參加社區服務時間是否超過1小時與性別有關？
（3）從該校學生中隨機調查60名學生，一周參加社區服務時間超過1小時的人數記為X，以樣本中學生參加社區服務時間超過1小時的頻率作為該事件發生的概率，求X的分布列和數學期望.
附：
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在長方體
中，
，
為
的中點，
為
的中點，
為線段
上一點，且滿足
，
為
的中點.
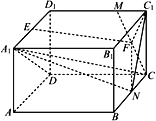
（1）求證：
平面
；
（2）求三棱錐
的體積；
（3）求直線
與直線
所成角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過曲線C1：
(a＞0，b＞0)的左焦點F1作曲線C2：x2＋y2＝a2的切線，設切點為M，直線F1M交曲線C3：y2＝2px(p＞0)于點N，其中曲線C1與C3有一個共同的焦點，若|MF1|＝|MN|，則曲線C1的離心率為( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義R在上的函數
為奇函數，并且其圖象關于x＝1對稱；當x∈（0，1]時，f（x）＝9x﹣3．若數列{an}滿足an＝f（log2（64+n））（n∈N+）；若n≤50時，當Sn＝a1+a2+…+an取的最大值時，n＝_____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量指數
是反映空氣狀況的指數，指數值趨小，表明空氣質量越好，下圖是某市10月1日-20日指數變化趨勢，下列敘述錯誤的是（ ）
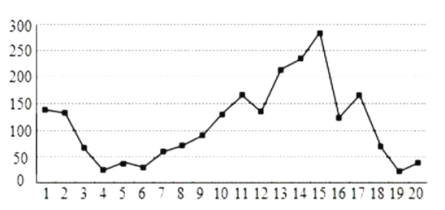
A.這20天中指數值的中位數略高于100
B.這20天中的中度污染及以上（指數
）的天數占
C.該市10月的前半個月的空氣質量越來越好
D.總體來說，該市10月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，曲線
方程為
，以極點為坐標原點，極軸為
軸正半軸的平面直角坐標系中，曲線
（
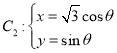為參數）
（1）將
化為直角坐標系中普通方程，并說明它們分別表示什么曲線；
（2）若極坐標系中上的點
對應的極角為
，
為
上的動點，求
中點
到直線
（
為參數）距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列
滿足
，其中
，且
， 
為常數.
（1）若
是等差數列，且公差
，求
的值；
（2）若
，且存在
，使得
對任意的
都成立，求
的最小值；
（3）若
，且數列
不是常數列，如果存在正整數
，使得
對任意的
均成立. 求所有滿足條件的數列
中
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com