
已知函數(shù) ,
, .
.
(1)若 ,判斷函數(shù)
,判斷函數(shù) 的奇偶性,并加以證明;
的奇偶性,并加以證明;
(2)若函數(shù) 在
在 上是增函數(shù),求實數(shù)
上是增函數(shù),求實數(shù) 的取值范圍;
的取值范圍;
(3)若存在實數(shù) 使得關于
使得關于 的方程
的方程 有三個不相等的實數(shù)根,求實數(shù)
有三個不相等的實數(shù)根,求實數(shù) 的取值范圍.
的取值范圍.
(1)奇函數(shù),(2) ,(3)
,(3) 
【解析】
試題分析:(1)函數(shù)奇偶性的判定,一要判定定義域是否關于原點對稱,二要判定 與
與 是否相等或相反,(2)函數(shù)
是否相等或相反,(2)函數(shù) 是分段函數(shù),每一段都是二次函數(shù)的一部分,因此研究
是分段函數(shù),每一段都是二次函數(shù)的一部分,因此研究 單調(diào)性,必須研究它們的對稱軸,從圖像可觀察得到實數(shù)
單調(diào)性,必須研究它們的對稱軸,從圖像可觀察得到實數(shù) 滿足的條件:
滿足的條件: ,(3)研究方程根的個數(shù),通常從圖像上研究,結合(2)可研究出函數(shù)
,(3)研究方程根的個數(shù),通常從圖像上研究,結合(2)可研究出函數(shù) 圖像.分三種情況研究,一是
圖像.分三種情況研究,一是 上單調(diào)增函數(shù),二是先在
上單調(diào)增函數(shù),二是先在 上單調(diào)增,后在
上單調(diào)增,后在 上單調(diào)減,再在
上單調(diào)減,再在 上單調(diào)增,三是先在
上單調(diào)增,三是先在 上單調(diào)增,后在
上單調(diào)增,后在 上單調(diào)減,再在
上單調(diào)減,再在 上單調(diào)增.
上單調(diào)增.
試題解析:(1)函數(shù) 為奇函數(shù).[來
為奇函數(shù).[來
當 時,
時, ,
, ,∴
,∴
∴函數(shù) 為奇函數(shù); 3分
為奇函數(shù); 3分
(2) ,當
,當 時,
時, 的對稱軸為:
的對稱軸為: ;
;
當 時,
時, 的對稱軸為:
的對稱軸為: ;∴當
;∴當 時,
時, 在R上是增函數(shù),即
在R上是增函數(shù),即 時,函數(shù)
時,函數(shù) 在
在 上是增函數(shù); 7分
上是增函數(shù); 7分
(3)方程 的解即為方程
的解即為方程 的解.
的解.
①當 時,函數(shù)
時,函數(shù) 在
在 上是增函數(shù),∴關于
上是增函數(shù),∴關于 的方程
的方程 不可能有三個不相等的實數(shù)根; 9分
不可能有三個不相等的實數(shù)根; 9分
②當 時,即
時,即 ,∴
,∴ 在
在 上單調(diào)增,在
上單調(diào)增,在 上單調(diào)減,在
上單調(diào)減,在 上單調(diào)增,∴當
上單調(diào)增,∴當 時,關于
時,關于 的方程
的方程 有三個不相等的實數(shù)根;即
有三個不相等的實數(shù)根;即 ,∵
,∵ ∴
∴ .
.
設 ,∵存在
,∵存在 使得關于
使得關于 的方程
的方程 有三個不相等的實數(shù)根, ∴
有三個不相等的實數(shù)根, ∴ ,又可證
,又可證 在
在 上單調(diào)增
上單調(diào)增
∴ ∴
∴ ; 12分
; 12分
③當 時,即
時,即 ,∴
,∴ 在
在 上單調(diào)增,在
上單調(diào)增,在 上單調(diào)減,在
上單調(diào)減,在 上單調(diào)增,
上單調(diào)增,
∴當 時,關于
時,關于 的方程
的方程 有三個不相等的實數(shù)根;
有三個不相等的實數(shù)根;
即 ,∵
,∵ ∴
∴ ,設
,設
∵存在 使得關于
使得關于 的方程
的方程 有三個不相等的實數(shù)根,
有三個不相等的實數(shù)根,
∴ ,又可證
,又可證 在
在 上單調(diào)減∴
上單調(diào)減∴
∴ ; 15分
; 15分
綜上: . 16分
. 16分
考點:函數(shù)奇偶性,函數(shù)單調(diào)性,函數(shù)與方程.


 活力試卷系列答案
活力試卷系列答案 課課優(yōu)能力培優(yōu)100分系列答案
課課優(yōu)能力培優(yōu)100分系列答案科目:高中數(shù)學 來源:2016屆江蘇省高一上學期期中考試數(shù)學試卷(解析版) 題型:填空題
設函數(shù) 的定義域為
的定義域為 ,如果存在正實數(shù)
,如果存在正實數(shù) ,對于任意
,對于任意 都有
都有 ,且
,且 恒成立,則稱函數(shù)
恒成立,則稱函數(shù) 為
為 上的“
上的“ 型增函數(shù)”。已知函數(shù)
型增函數(shù)”。已知函數(shù)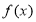 是定義在
是定義在 上的奇函數(shù),且當
上的奇函數(shù),且當 時,
時, ,若
,若 為
為 上的“
上的“ 型增函數(shù)”,則實數(shù)
型增函數(shù)”,則實數(shù) 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學 來源:2016屆江蘇省揚州市高一上學期期末調(diào)研測試數(shù)學試卷(解析版) 題型:解答題
已知 ,且
,且 是第一象限角.
是第一象限角.
(1)求 的值;
的值;
(2)求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源:2016屆江蘇省徐州市高一第一學期期末試卷數(shù)學試卷(解析版) 題型:填空題
若函數(shù) 在其定義域上為奇函數(shù),則實數(shù)
在其定義域上為奇函數(shù),則實數(shù) .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com