解:(1)設t=

,任取x
2<x
1<-5,則
t
2-t
1=

-

=

=

.
∵x
1<-5,x
2<-5,x
2<x
1,
∴x
1+5<0,x
2+5<0,x
2-x
1<0.
∴

<0,即t
2<t
1.
當a>1時,y=log
ax是增函數,∴log
at
2<log
at
1,即f(x
2)<f(x
1);
當0<a<1時,y=log
ax是減函數,∴log
at
2>log
at
1,即f(x
2)>f(x
1).
綜上可知,當a>1時,f(x)在區間(-∞,-5)為增函數;
當0<a<1時,f(x)在區間(-∞,-5)為減函數.
(2)g(x)=1+log
a(x-3)=log
aa(x-3),
方程f(x)=g(x)等價于:

即方程
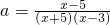
在區間(5,+∞)上有解,
∵

=

∴函數F(x)=
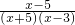
在區間(5,5+2

)上導數大于零,在區間(5+2

,+∞)導數小于零
可得F(x)=
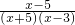
在區間(5,5+2

)上單調增,在區間(5+2

,+∞)單調減
∴F(x)的最大值為F(5+2

)=

,而F(x)的最小值大于F(5)=0
要使方程方程
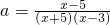
在區間(5,+∞)上有解,必須a∈(0,

)
所以a的取值范圍是:(0,

)
分析:(1)將對數的真數當成一個函數,可以用定義證明它在區間(-∞,-5)內的單調性,再討論底數a與1的大小關系得到相應的情況下真數的大小關系,即可得函數f(x)在區間(-∞,-5)內的單調性;
(2)化函數g(x)=1+log
a(x-3))為g(x)=log
aa(x-3),方程f(x)=g(x)即為它們的真數都大于零且相等,采用變量分離的方法,轉化為求函數F(x)=
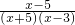
在區間(5,+∞)上的值域,實數a的取值范圍就應該屬于這個值域.
點評:本題著重考查了函數單調性的判斷與證明、根的存在性及根的個數判斷等知識點,在解題時應該注意分類討論與數形結合等數學思想的應用.

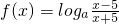
 ,任取x2<x1<-5,則
,任取x2<x1<-5,則 -
-

 .
. <0,即t2<t1.
<0,即t2<t1.
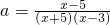 在區間(5,+∞)上有解,
在區間(5,+∞)上有解, =
=
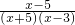 在區間(5,5+2
在區間(5,5+2 )上導數大于零,在區間(5+2
)上導數大于零,在區間(5+2 ,+∞)導數小于零
,+∞)導數小于零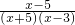 在區間(5,5+2
在區間(5,5+2 )上單調增,在區間(5+2
)上單調增,在區間(5+2 ,+∞)單調減
,+∞)單調減 )=
)= ,而F(x)的最小值大于F(5)=0
,而F(x)的最小值大于F(5)=0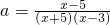 在區間(5,+∞)上有解,必須a∈(0,
在區間(5,+∞)上有解,必須a∈(0, )
) )
)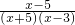 在區間(5,+∞)上的值域,實數a的取值范圍就應該屬于這個值域.
在區間(5,+∞)上的值域,實數a的取值范圍就應該屬于這個值域.

