
【題目】設點![]() ,
,![]() ,
,![]() 為坐標原點,點
為坐標原點,點![]() 滿足
滿足![]() =
=![]() +
+![]() ,(
,(![]() 為實數);
為實數);
(1)當點![]() 在
在![]() 軸上時,求實數
軸上時,求實數![]() 的值;
的值;
(2)四邊形![]() 能否是平行四邊形?若是,求實數
能否是平行四邊形?若是,求實數![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
【答案】(1)![]() (2)四邊形OABP不是平行四邊形
(2)四邊形OABP不是平行四邊形
【解析】
試題分析:(1)設點P(x,0),由![]() =
=![]() +
+![]() 得(x,0)=(2,2)+t(3,2 ),解出t值.(2),設點P(x,y),假設四邊形OABP是平行四邊形,根據向量平行得出坐標間的關系,由
得(x,0)=(2,2)+t(3,2 ),解出t值.(2),設點P(x,y),假設四邊形OABP是平行四邊形,根據向量平行得出坐標間的關系,由![]() =
=![]() +
+![]() ,推出矛盾,故假設是錯誤的
,推出矛盾,故假設是錯誤的
試題解析:(1)設點P(x,0), ![]() =(3,2),
=(3,2),
∵![]() =
=![]() +
+![]() ,∴ (x,0)=(2,2)+t(3,2),
,∴ (x,0)=(2,2)+t(3,2),
![]() ∴
∴ ![]()
(2)設點P(x,y),假設四邊形OABP是平行四邊形,
則有![]() ∥
∥![]() , y=x―1,
, y=x―1, ![]() ∥
∥![]() 2y=3x
2y=3x ![]() ……①,
……①,
又由![]() =
=![]() +
+![]() , (x,y)=(2,2)+ t(3,2),得 ∴
, (x,y)=(2,2)+ t(3,2),得 ∴ ![]() ……②,
……②,
由①代入②得: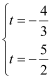 , 矛盾,∴假設是錯誤的,
, 矛盾,∴假設是錯誤的,
∴四邊形OABP不是平行四邊形。


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】關于for x=a:b:c,下列說法正確的有( )
①當x=c時程序結束;②當x=c時,還要繼續執行一次;③當b>0時,x≥a時程序結束;④當b<0時,x<a時程序結束.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,C.已知3cos(B-C)-1=6cosBcosC.
(1)求cosA;
(2)若a=3,△ABC的面積為![]() ,求邊b和c.
,求邊b和c.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,過頂點在原點![]() ,對稱軸為
,對稱軸為![]() 軸的拋物線
軸的拋物線![]() 上的定點
上的定點![]() 作斜率分別為
作斜率分別為![]() 的直線,分別交拋物線
的直線,分別交拋物線![]() 于
于![]() 兩點.
兩點.
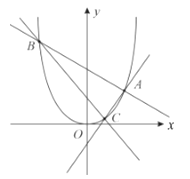
(1)求拋物線![]() 的標準方程和準線方程;
的標準方程和準線方程;
(2)若![]() ,且
,且![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四種說法:
①兩個相交平面有不在同一直線上的三個公共點;②一條直線和一個點確定一個平面;③若四點不共面, 則每三點一定不共線; ④三條平行線確定三個平面.正確說法的個數為( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知市場上供應的燈泡中,甲廠產品占70%,乙廠占30%,甲廠產品的合格率是95%,乙廠產品的合格率是80%,則從市場上買到一個是甲廠生產的合格燈泡的概率是( )
A. 0.665 B. 0.56 C. 0.24 D. 0.028 5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王在年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為25-x萬元(國家規定大貨車的報廢年限為10年).
(1)大貨車運輸到第幾年年底,該車運輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大(利潤=累計收入+銷售收入-總支出)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】讀下面的甲、乙兩個程序:
i=1;
S=0;
while i<=1000
S=S+i;
i=i+1;
end
甲
i=1000;
S=0;
for i=1000:-1:1
S=S+i;
end
乙
對甲、乙兩個程序和輸出的結果判斷正確的是( )
A. 程序不同,結果不同
B. 程序不同,結果相同
C. 程序相同,結果不同
D. 程序相同,結果相同
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com