【題目】已知
是各項均為正數的等比數列，
.
（1）求的通項公式；
（2）設
，求數列
的前n項和.
【答案】（1）
；（2）
.
【解析】
(1)本題首先可以根據數列
是等比數列將
轉化為
，
轉化為
，再然后將其帶入
中，并根據數列是各項均為正數以及
即可通過運算得出結果；
(2)本題可以通過數列的通項公式以及對數的相關性質計算出數列
的通項公式，再通過數列的通項公式得知數列是等差數列，最后通過等差數列求和公式即可得出結果。
(1)因為數列是各項均為正數的等比數列，，，
所以令數列的公比為
，
，
，
所以
，解得
(舍去)或
，
所以數列是首項為
、公比為的等比數列，
。
(2)因為
，所以
，
，
，
所以數列是首項為
、公差為的等差數列，
。
本題考查數列的相關性質，主要考查等差數列以及等比數列的通項公式的求法，考查等差數列求和公式的使用，考查化歸與轉化思想，考查計算能力，是簡單題。
快樂暑假暑假能力自測中西書局系列答案科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱ABC﹣A1B1C1中，E，F分別為A1C1和BC的中點，M，N分別為A1B和A1C的中點.求證：
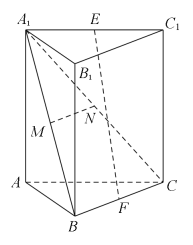
（1）MN∥平面ABC；
（2）EF∥平面AA1B1B.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
與
軸相切于點
，且被
軸所截得的弦長為
，圓心在第一象限.
（Ⅰ）求圓的方程；
（Ⅱ）若點
是直線
上的動點，過作圓的切線，切點為
，當△
的面積最小時，求切線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校從高一年級參加期末考試的學生中抽出60名，其成績(均為整數)的頻率分布直方圖如圖所示，由此估計此次考試成績的中位數、眾數分別是（ ）
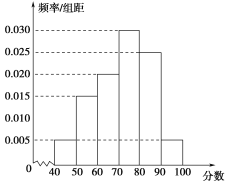
A.73.3，75B.73.3，80
C.70，70D.70， 75
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】小王大學畢業后，決定利用所學專業進行自主創業.經過市場調查，生產某小型電子產品需投入年固定成本3萬元，每生產x萬件，該產品需另投入流動成本
萬元.在年產量不足8萬件時，
，在年產量不小于8萬件時，
每件產品的售價為5元.通過市場分析，小王生產的商品能當年全部售完.
（1）寫出年利潤
單位：萬元
關于年產量
單位：萬件的函數解析式.
（2）年產量為多少萬件時，小王在這一商品的生產中所獲利潤最大？最大利潤是多少？
注：年利潤
年銷售收入
固定成本流動成本
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某高校共有15000人，其中男生10500人，女生4500人，為調查該校學生每周平均體育運動時間的情況，采用分層抽樣的方法，收集300位學生每周平均體育運動時間的樣本數據（單位:小時）
（1）應收集多少位女生樣本數據？
（2）根據這300個樣本數據，得到學生每周平均體育運動時間的頻率分布直方圖（如圖所示），其中樣本數據分組區間為：
.估計該校學生每周平均體育運動時間超過4個小時的概率.
（3）在樣本數據中，有60位女生的每周平均體育運動時間超過4個小時.請完成每周平均體育運動時間與性別的列聯表，并判斷是否有
的把握認為“該校學生的每周平均體育運動時間與性別有關”.
附：
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
以平面直角坐標系
的原點為極點， 
軸的正半軸為極軸，建立極坐標系，兩種坐標系中取相同的長度單位，直線
的參數方程為
（
為參數），圓
的極坐標方程為
.
（1）求直線
的普通方程與圓
的直角坐標方程；
（2）設曲線
與直線
交于
兩點，若
點的直角坐標為
，求
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
