
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求證:M為PB的中點;
(II)求二面角B-PD-A的大小;
(III)求直線MC與平面BDP所成角的正弦值.

【答案】(1)見解析(2)![]() (3)
(3)![]()
【解析】試題分析:(Ⅰ)設![]() 交點為
交點為![]() ,連接
,連接![]() ,因為線面平行,即
,因為線面平行,即![]() 平面
平面![]() ,根據性質定理,可知線線平行,即
,根據性質定理,可知線線平行,即![]() ,再由
,再由![]() 為
為![]() 的中點,可知
的中點,可知![]() 為
為![]() 的中點;(Ⅱ)因為平面
的中點;(Ⅱ)因為平面![]() 平面
平面![]() ,
, ![]() ,所以取
,所以取![]() 的中點
的中點![]() 為原點建立空間直角坐標系,根據向量法先求兩平面的法向量
為原點建立空間直角坐標系,根據向量法先求兩平面的法向量![]() ,
, ![]() ,再根據公式
,再根據公式![]() ,求二面角的大小;(Ⅲ)根據(Ⅱ)的結論,直接求
,求二面角的大小;(Ⅲ)根據(Ⅱ)的結論,直接求![]() 即可.
即可.
試題解析:解:(I)設![]() 交點為
交點為![]() ,連接
,連接![]() .
.
因為![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因為![]() 是正方形,所以
是正方形,所以![]() 為
為![]() 的中點,所以
的中點,所以![]() 為
為![]() 的中點.
的中點.
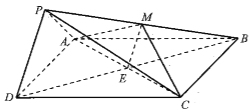
(II)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
, ![]() .
.
因為![]() ,所以
,所以![]() .
.
又因為平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,所以
,所以![]() .
.
因為![]() 是正方形,所以
是正方形,所以![]() .
.
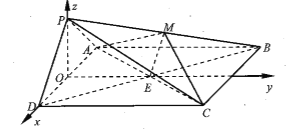
如圖建立空間直角坐標系![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,即
,即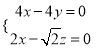 .
.
令![]() ,則
,則![]() ,
, ![]() .于是
.于是![]() .
.
平面![]() 的法向量為
的法向量為![]() ,所以
,所以![]() .
.
由題知二面角![]() 為銳角,所以它的大小為
為銳角,所以它的大小為![]() .
.
(III)由題意知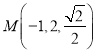 ,
, ![]() ,
, 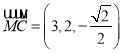 .
.
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則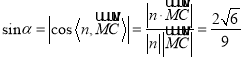 .
.
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為梯形,PD⊥底面ABCD,AB∥CD,AD⊥CD,AD=AB=1,BC=![]() .
.
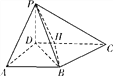
(Ⅰ)求證:平面PBD⊥平面PBC;
(Ⅱ)設H為CD上一點,滿足![]() =2
=2![]() ,若直線PC與平面PBD所成的角的正切值為
,若直線PC與平面PBD所成的角的正切值為![]() ,求二面角H-PB-C的余弦值.
,求二面角H-PB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某批次的某種燈泡![]() 個,對其壽命進行追蹤調查,將結果列成頻率分布表如下,根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于
個,對其壽命進行追蹤調查,將結果列成頻率分布表如下,根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于![]() 天的燈泡是優等品,壽命小于
天的燈泡是優等品,壽命小于![]() 天的燈泡是次品,其余的燈泡是正品.
天的燈泡是次品,其余的燈泡是正品.
壽命 (天) | 頻數 | 頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合計 |
|
|
(1)根據頻率分布表中的數據,寫出![]() 的值;
的值;
(2)某人從這![]() 個燈泡中隨機地購買了
個燈泡中隨機地購買了![]() 個,求此燈泡恰好不是次品的概率;
個,求此燈泡恰好不是次品的概率;
(3)某人從這批燈泡中隨機地購買了![]() 個,如果這
個,如果這![]() 個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求
個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某校舉行歌唱比賽時,七位評委為某位選手打出的分數的莖葉統計圖,去掉一個最高分和一個最低分后,所剩數據的中位數和平均數依次為( ) 
A.87,86
B.83,85
C.88,85
D.82,86
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某旅游愛好者計劃從3個亞洲國家A1,A2,A3和3個歐洲國家B1,B2,B3中選擇2個國家去旅游.
(1)若從這6個國家中任選2個,求這2個國家都是亞洲國家的概率;
(2)若從亞洲國家和歐洲國家中各選1個,求這兩個國家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 和
和![]() 是兩個等差數列,記
是兩個等差數列,記![]()
![]() ,
,
其中![]() 表示
表示![]() 這
這![]() 個數中最大的數.
個數中最大的數.
(Ⅰ)若![]() ,
, ![]() ,求
,求![]() 的值,并證明
的值,并證明![]() 是等差數列;
是等差數列;
(Ⅱ)證明:或者對任意正數![]() ,存在正整數
,存在正整數![]() ,當
,當![]() 時,
時, ![]() ;或者存在正整數
;或者存在正整數![]() ,使得
,使得![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
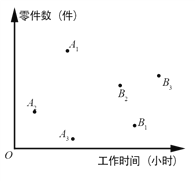
【題目】三名工人加工同一種零件,他們在一天中的工作情況如圖所示,其中點Ai的橫、縱坐標分別為第i名工人上午的工作時間和加工的學科&網零件數,點Bi的橫、縱坐標分別為第i名工人下午的工作時間和加工的零件數,i=1,2,3.
①記Qi為第i名工人在這一天中加工的零件總數,則Q1,Q2,Q3中最大的是_________.
②記pi為第i名工人在這一天中平均每小時加工的零件數,則p1,p2,p3中最大的是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x)定義域中任意的x1 , x2(x1≠x2),有如下結論:
(1)f(x1+x2)=f(x1)f(x2)
(2)f(x1x2)=f(x1)+f(x2)
(3) ![]()
當f(x)=ex時,上述結論中正確結論的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,點P是圓x2+y2=4上一動點,PD⊥x軸于點D,記滿足 ![]() =
= ![]() (
( ![]() +
+ ![]() )的動點M的軌跡為Γ. (Ⅰ)求軌跡Γ的方程;
)的動點M的軌跡為Γ. (Ⅰ)求軌跡Γ的方程;
(Ⅱ)已知直線l:y=kx+m與軌跡F交于不同兩點A,B,點G是線段AB中點,射線OG交軌跡Γ于點Q,且 ![]() =λ
=λ ![]() ,λ∈R.
,λ∈R.
①證明:λ2m2=4k2+1;
②求△AOB的面積S(λ)的解析式,并計算S(λ)的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com