【題目】在如圖所示的幾何體中，四邊形
是等腰梯形，
∥
，
平面
.
（Ⅰ）求證：
平面
；
（Ⅱ）求二面角
的余弦值.
【答案】：（Ⅰ）見解析；（Ⅱ）
【解析】
試題分析：（1）要證明直線和平面垂直，只需證明直線和平面內的兩條相交直線垂直．由已知得
，故只需證明
，在
中，由余弦定理得
的關系，即
的關系確定，在
中，結合已知條件
可判定是直角三角形，且，從而可證明BD⊥平面AED；（2）求二面角
，可先找后求，過
作
，由已知FC⊥平面ABCD，得
面
，故，
，故
為二面角F—BD—C的平面角，在
中計算．
（1）在等腰梯形ABCD中，AB∥CD，∠DAB= 60°，
，由余弦定理可知，
，即
，在中，，
，則是直角三角形，且，又，且
，故BD⊥平面AED．
（2）過作，交
于點
，因為FC⊥平面ABCD，
面
，所以
，所以
面，因此，，故為二面角F—BD—C的平面角.
在
中，
，可得
因此
. 即二面角F—BD—C的正切值為2.
輕巧奪冠周測月考直通名校系列答案科目：高中數學 來源： 題型：
【題目】為比較甲、乙兩地某月14時的氣溫狀況，隨機選取該月中的5天，將這5天中14時的氣溫數據（單位：℃）制成如圖所示的莖葉圖．考慮以下結論：
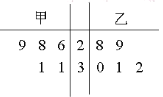
①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫；
②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫；
③甲地該月14時的平均氣溫的標準差小于乙地該月14時的氣溫的標準差；
④甲地該月14時的平均氣溫的標準差大于乙地該月14時的氣溫的標準差．
其中根據莖葉圖能得到的統計結論的標號為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直三棱柱A1B1C1﹣ABC中， 
，AB=AC=AA1=1，已知G和E分別為A1B1和CC1的中點，D與F分別為線段AC和AB上的動點（不包括端點），若GD⊥EF，則線段DF的長度的取值范圍為（ ）
A.[ 
，1）
B.[ ，1]
C.（ 
，1）
D.[ ，1）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
：
（
為參數），曲線
：
（
為參數）.
（1）設與相交于
，
兩點，求
的值；
（2）若把曲線上各點的橫坐標壓縮為原來的
，縱坐標壓縮為原來的
，得到曲線
，設點
是曲線上的一個動點，求它到直線的距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線 
與雙曲線 
的離心率相同，且雙曲線C2的左、右焦點分別為F1 ， F2 ， M是雙曲線C2一條漸近線上的某一點，且OM⊥MF2 ， 
，則雙曲線C2的實軸長為（ ）
A.4
B.
C.8
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】秦九韶是我國南宋時期的數學家，他在所著的《數學九章》中提出的多項式求值的秦九韶算法，至今仍是比較先進的算法，如圖所示的程序框圖給出了利用秦九韶算法求某多項式值的一個實例，若輸入n，x的值分別為4，2，則輸出v的值為（ ） 
A.66
B.33
C.16
D.8
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現給出以下四個命題：
①已知
中，角A，B，C的對邊為a，b，c，當
，
，
時，滿足條件的三角形共有1個；
②已知中，角A，B，C的對邊為a，b，c，若三角形
，這個三角形的最大角是
；
③設
是兩條不同的直線，
，
是兩個不同的平面,若
，
，則
；
④設是兩條不同的直線，，是兩個不同的平面,若
，
，則
其中正確的序號是__________（寫出所有正確說法的序號）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-5：不等式選講]
已知函數f（x）=﹣x2+ax+4，g（x）=|x+1|+|x﹣1|．（10分）
（1）當a=1時，求不等式f（x）≥g（x）的解集；
（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
