
【題目】已知函數f(x)=xlnx,g(x)=x+ ![]() (x>0)都在x=x0處取得最小值.
(x>0)都在x=x0處取得最小值.
(1)求f(x0)﹣g(x0)的值.
(2)設函數h(x)=f(x)﹣g(x),h(x)的極值點之和落在區間(k,k+1),k∈N,求k的值.
【答案】
(1)解:∵f(x)=xlnx,x>0,
∴f′(x)=1+lnx,
令f′(x)=1+lnx=0,解得x= ![]() ,
,
當x> ![]() 時,f′(x)>0,函數f(x)單調遞增,
時,f′(x)>0,函數f(x)單調遞增,
當0<x< ![]() 時,f′(x)<0,函數f(x)單調遞減,
時,f′(x)<0,函數f(x)單調遞減,
∴當x= ![]() ,且f(
,且f( ![]() )=﹣
)=﹣ ![]() ,
,
∵f(x)=xlnx,g(x)=x+ ![]() (x>0)都在x=x0處取得最小值,
(x>0)都在x=x0處取得最小值,
∴x0= ![]() ,
,
∵g(x)=x+ ![]() (x>0),
(x>0),
∴g′(x)=1﹣ ![]() ,
,
∴g′( ![]() )=1﹣
)=1﹣ ![]() =0,
=0,
解得a=e2,
∴g(x0)=g( ![]() )=
)= ![]() +
+ ![]() ,
,
∴f(x0)﹣g(x0)=﹣ ![]() +
+ ![]() +
+ ![]() =
= ![]()
(2)解:函數h(x)=f(x)﹣g(x)=xlnx﹣x﹣ ![]() ,
,
∴h′(x)=1+lnx﹣1+ ![]() =lnx﹣
=lnx﹣ ![]() ,
,
設φ(x)=lnx﹣ ![]() ,
,
∴φ′(x)= ![]() +
+ ![]() >0,
>0,
∴h′(x)在(0,+∞)上單調遞增,
∴h′(1)h(e)<0,
∴h′(x)在(1,e)上存在唯一的零點,
∵h(x)的極值點之和落在區間(k,k+1),
∴k=1
【解析】(1)先利用導數求出f(x)的極值點和極值,繼而求出a的值,再求出g(x)的極值,問題得以解決,(2)先求導得到h′(x)=lnx﹣ ![]() ,再根據函數零點存在定理即可判斷零點所在的區間.
,再根據函數零點存在定理即可判斷零點所在的區間.
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的極值與導數,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值才能得出正確答案.
是極小值才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】已知A是拋物線y2=4x上的一點,以點A和點B(2,0)為直徑的圓C交直線x=1于M,N兩點.直線l與AB平行,且直線l交拋物線于P,Q兩點. 
(Ⅰ)求線段MN的長;
(Ⅱ)若 ![]() =﹣3,且直線PQ與圓C相交所得弦長與|MN|相等,求直線l的方程.
=﹣3,且直線PQ與圓C相交所得弦長與|MN|相等,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(ax+1)﹣ax﹣lna.
(1)討論f(x)的單調性;
(2)若h(x)=ax﹣f(x),當h(x)>0恒成立時,求a的取值范圍;
(3)若存在 ![]() ,x2>0,使得f(x1)=f(x2)=0,判斷x1+x2與0的大小關系,并說明理由.
,x2>0,使得f(x1)=f(x2)=0,判斷x1+x2與0的大小關系,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】漳州水仙鱗莖碩大,箭多花繁,色美香郁,素雅娟麗,有“天下水仙數漳州”之美譽.現某水仙花雕刻師受雇每天雕刻250粒水仙花,雕刻師每雕刻一粒可賺1.2元,如果雕刻師當天超額完成任務,則超出的部分每粒多賺0.5元;如果當天未能按量完成任務,則按完成的雕刻量領取當天工資. (Ⅰ)求雕刻師當天收入(單位:元)關于雕刻量n(單位:粒,n∈N)的函數解析式f(n);
(Ⅱ)該雕刻師記錄了過去10天每天的雕刻量n(單位:粒),整理得如表:
雕刻量n | 210 | 230 | 250 | 270 | 300 |
頻數 | 1 | 2 | 3 | 3 | 1 |
以10天記錄的各雕刻量的頻率作為各雕刻量發生的概率.
(ⅰ)在當天的收入不低于276元的條件下,求當天雕刻量不低于270個的概率;
(ⅱ)若X表示雕刻師當天的收入(單位:元),求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=(x﹣a)(x﹣b)(x﹣c)(其中a>1,b>1),x=0是f(x)的一個零點,曲線y=f(x)在點(1,f(1))處的切線平行于x軸,則a+b的最小值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】斐波那契數列{an}滿足: ![]() .若將數列的每一項按照下圖方法放進格子里,每一小格子的邊長為1,記前n項所占的格子的面積之和為Sn , 每段螺旋線與其所在的正方形所圍成的扇形面積為cn , 則下列結論錯誤的是( )
.若將數列的每一項按照下圖方法放進格子里,每一小格子的邊長為1,記前n項所占的格子的面積之和為Sn , 每段螺旋線與其所在的正方形所圍成的扇形面積為cn , 則下列結論錯誤的是( ) 
A.![]()
B.a1+a2+a3+…+an=an+2﹣1
C.a1+a3+a5+…+a2n﹣1=a2n﹣1
D.4(cn﹣cn﹣1)=πan﹣2an+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在幾何體ABCDEF中,底面ABCD為矩形,EF∥CD,AD⊥FC.點M在棱FC上,平面ADM與棱FB交于點N. 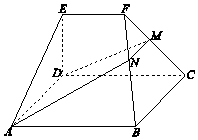
(Ⅰ)求證:AD∥MN;
(Ⅱ)求證:平面ADMN⊥平面CDEF;
(Ⅲ)若CD⊥EA,EF=ED,CD=2EF,平面ADE∩平面BCF=l,求二面角A﹣l﹣B的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中有如下問題:“今有女子善織,日益功,疾,初日織五尺,今一月織九匹三丈(1匹=40尺,一丈=10尺),問日益幾何?”其意思為:“有一女子擅長織布,每天比前一天更加用功,織布的速度也越來越快,從第二天起,每天比前一天多織相同量的布,第一天織5尺,一月織了九匹三丈,問每天增加多少尺布?”若一個月按31天算,記該女子一個月中的第n天所織布的尺數為an , 則 ![]() 的值為( )
的值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com