
【題目】已知函數![]()
![]() 的圖像如圖所示.
的圖像如圖所示.

(1)求函數的解析式;
(2)當![]() 時,求函數
時,求函數![]() 的最大值和最小值.
的最大值和最小值.
科目:高中數學 來源: 題型:
【題目】函數![]() 的定義域為D,若存在閉區間
的定義域為D,若存在閉區間![]()
![]() ,使得函數
,使得函數![]() 同時滿足:
同時滿足:
(1)![]() 在
在![]() 內是單調函數;
內是單調函數;
(2)![]() 在
在![]() 上的值域為
上的值域為![]() ,則稱區間
,則稱區間![]() 為
為![]() 的“
的“![]() 倍值區間”.
倍值區間”.
下列函數中存在“3倍值區間”的有_____.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
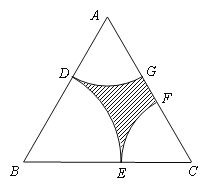
【題目】近年來,隨著我市經濟的快速發展,政府對民生也越來越關注. 市區現有一塊近似正三角形土地ABC(如圖所示),其邊長為2百米,為了滿足市民的休閑需求,市政府擬在三個頂點處分別修建扇形廣場,即扇形DBE,DAG和ECF,其中![]() 、
、![]() 與
與![]() 分別相切于點D、E,且
分別相切于點D、E,且![]() 與
與![]() 無重疊,剩余部分(陰影部分)種植草坪. 設BD長為x(單位:百米),草坪面積為S(單位:百米2).
無重疊,剩余部分(陰影部分)種植草坪. 設BD長為x(單位:百米),草坪面積為S(單位:百米2).
(1)試用x分別表示扇形DAG和DBE的面積,并寫出x的取值范圍;
(2)當x為何值時,草坪面積最大?并求出最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數.
為奇函數.
(1)求常數![]() 的值;
的值;
(2)設![]() ,證明函數
,證明函數![]() 在(1,+∞)上是減函數;
在(1,+∞)上是減函數;
(3)若函數![]() ,且
,且![]() 在區間[3,4]上沒有零點,求實數
在區間[3,4]上沒有零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E是A1B1上一點,若平面EBD與平面ABCD所成銳二面角的正切值為 ![]() ,設三棱錐A﹣A1D1E外接球的直徑為a,則
,設三棱錐A﹣A1D1E外接球的直徑為a,則 ![]() = .
= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,PA⊥底面ABCD,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,PA= ![]() a,AD=2a.
a,AD=2a.
(1)若AE⊥PD,E為垂足,求異面直線AE與CD所成角的余弦值;
(2)求平面PAB與平面PCD所成的銳二面角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐A﹣BCD的所有棱長均為6,點P在AC上,且AP=2PC,過P作四面體的截面,使截面平行于直線AB和CD,則該截面的周長為( )
A.16
B.12
C.10
D.8
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓A:(x+1)2+y2=8,動圓M經過點B(1,0),且與圓A相切,O為坐標原點.
(Ⅰ)求動圓圓心M的軌跡C的方程;
(Ⅱ)直線l與曲線C相切于點M,且l與x軸、y軸分別交于P、Q兩點,若 ![]() =λ
=λ ![]() ,且λ∈[
,且λ∈[ ![]() ,2],求△OPQ面積S的取值范圍.
,2],求△OPQ面積S的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,根據長期收益率市場預測,投資![]() 類產品的收益與投資額成正比,投資
類產品的收益與投資額成正比,投資![]() 類產品的收益與投資額的算術平方根成正比.已知投資1萬元時
類產品的收益與投資額的算術平方根成正比.已知投資1萬元時![]() 兩類產品的收益分別為0.125萬元和0.5萬元.
兩類產品的收益分別為0.125萬元和0.5萬元.
(1)分別寫出![]() 兩類產品的收益與投資額的函數關系;
兩類產品的收益與投資額的函數關系;
(2)該家庭有20萬元資金,全部用于理財投資,問:怎么分配資金能使投資獲得最大收益,其最大收益是多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com