
【題目】如圖所示是某企業(yè)2010年至2016年污水凈化量(單位: 噸)的折線圖.
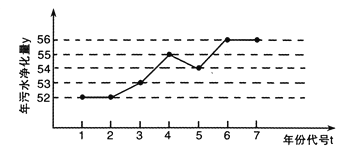
注: 年份代碼1-7分別對應年份2010-2016.
(1)由折線圖看出,可用線性回歸模型擬合![]() 和
和![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程,預測
的回歸方程,預測![]() 年該企業(yè)污水凈化量;
年該企業(yè)污水凈化量;
(3)請用數據說明回歸方程預報的效果.
附注: 參考數據:![]() ;
;
參考公式:相關系數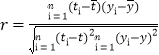 ,回歸方程
,回歸方程![]() 中斜率和截距的最小;
中斜率和截距的最小;
二乘法估汁公式分別為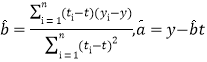 ;
;
反映回歸效果的公式為: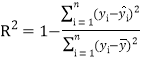 ,其中
,其中![]() 越接近于
越接近于![]() ,表示回歸的效果越好.
,表示回歸的效果越好.
【答案】(1) 見解析;(2) 預測![]() 年該企業(yè)污水凈化量約為
年該企業(yè)污水凈化量約為![]() 噸;(3) 回歸方程預測的效果是良好的.
噸;(3) 回歸方程預測的效果是良好的.
【解析】試題分析:(1)先求![]() ,再將折線圖中的數據代入參考公式可得相關系數,最后根據數值進行判斷相關性, (2) 將折線圖中的數據代入參考公式可得
,再將折線圖中的數據代入參考公式可得相關系數,最后根據數值進行判斷相關性, (2) 將折線圖中的數據代入參考公式可得![]() ,再根據線性回歸方程恒過
,再根據線性回歸方程恒過![]() ,解出
,解出![]() ,最后求
,最后求![]() 所對應函數值
所對應函數值![]() ,(3) 將折線圖中的數據代入參考公式可得
,(3) 將折線圖中的數據代入參考公式可得![]() ,再根據數據說明預測的效果.
,再根據數據說明預測的效果.
試題解析:(1) 由折線圖中的數據和附注中的參考數據得,
![]() ,所以
,所以![]() .因為
.因為![]() 與
與![]() 的相關系數近似為
的相關系數近似為![]() ,說明
,說明![]() 與
與![]() 的線性相關程度相當大,從而可以用線性回歸模型擬合
的線性相關程度相當大,從而可以用線性回歸模型擬合![]() 與
與![]() 的關系.
的關系.
(2) 由![]() 及(1)得
及(1)得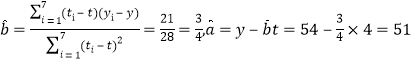 ,
,
所以![]() 關于
關于![]() 的回舊方程為:
的回舊方程為: ![]() , 將
, 將![]() 年對應的
年對應的![]() 代入得
代入得![]() ,
,
所以預測![]() 年該企業(yè)污水凈化量約為
年該企業(yè)污水凈化量約為![]() 噸.
噸.
(3) 因為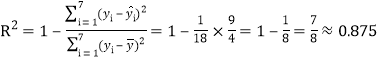 ,所以“污水凈化量的差異” 有
,所以“污水凈化量的差異” 有![]() 是由年份引起的,這說明回歸方程預測的效果是良好的.
是由年份引起的,這說明回歸方程預測的效果是良好的.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
某公司經銷某產品,第![]() 天
天![]() 的銷售價格為
的銷售價格為![]() (
(![]() 為常數)(元∕件),第
為常數)(元∕件),第![]() 天的銷售量為
天的銷售量為![]() (件),且公司在第
(件),且公司在第![]() 天該產品的銷售收入為
天該產品的銷售收入為![]() 元.
元.
(1)求該公司在第![]() 天該產品的銷售收入是多少?
天該產品的銷售收入是多少?
(2)這![]() 天中該公司在哪一天該產品的銷售收入最大?最大收入為多少?
天中該公司在哪一天該產品的銷售收入最大?最大收入為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
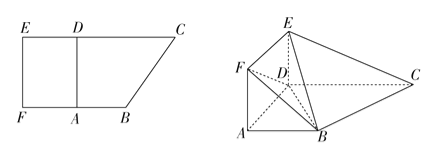
【題目】【2017銀川一中模擬】如圖,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.現以AD為一邊向梯形外作矩形ADEF,然后沿邊AD將矩形ADEF翻折,使平面ADEF與平面ABCD垂直.
CD=1.現以AD為一邊向梯形外作矩形ADEF,然后沿邊AD將矩形ADEF翻折,使平面ADEF與平面ABCD垂直.
(1)求證:BC⊥平面BDE;
(2)若點D到平面BEC的距離為![]() ,求三棱錐F-BDE的體積.
,求三棱錐F-BDE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,對任意實數
,對任意實數![]() ,都有
,都有![]() .
.
(1)若![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 為常數,函數
為常數,函數![]() 是奇函數,
是奇函數,
①驗證函數![]() 滿足題中的條件;
滿足題中的條件;
②若函數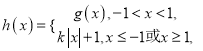 求函數
求函數![]() 的零點個數.
的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
喜愛打籃球 | 不喜愛打籃球 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 | 50 |
已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為![]() 。
。
(1)請將上面的列聯表補充完整;
(2)是否有99%的把握認為喜愛打籃球與性別有關?說明你的理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了實現60萬元的生源利潤目標,準備制定一個激勵招生人員的獎勵方案:在生源利潤達到5萬元時,按生源利潤進行獎勵,且資金y(單位:萬元)隨生源利潤x(單位:萬元)的增加而增加,但資金總數不超過3萬元,同時獎金不超過利潤的20%.現有三個獎勵模型:y=0.2x,y=log5x,y=1.02x,其中哪個模型符合該校的要求?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中點.
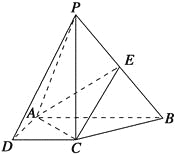
(1)求證:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值為![]() ,求直線PA與平面EAC所成角的正弦值.
,求直線PA與平面EAC所成角的正弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com