
【題目】已知函數![]() .
.
(1)求![]() 的單調區間與極值;
的單調區間與極值;
(2)當函數![]() 有兩個極值點時,求實數a的取值范圍.
有兩個極值點時,求實數a的取值范圍.
【答案】(1)減區間![]() ,增區間
,增區間 ![]() ,極小值為
,極小值為![]() ,無極大值;(2)
,無極大值;(2)![]() .
.
【解析】
(1)求出函數![]() 的導函數,根據導函數即可求出單調區間以及極值;
的導函數,根據導函數即可求出單調區間以及極值;
(2)求出![]() 的導函數,使導函數有兩個根,采用分離參數法,結合(1)中的值域即可求出參數的取值范圍.
的導函數,使導函數有兩個根,采用分離參數法,結合(1)中的值域即可求出參數的取值范圍.
解:(1)由![]() ,
,
則![]() ,
,
令![]() ,則
,則![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函數![]() 的單調遞增區間為
的單調遞增區間為![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函數![]() 的單調遞減區間為
的單調遞減區間為![]() ;
;
因為函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以函數在![]() 處取得極小值,
處取得極小值,![]() 極小值
極小值![]() ,無極大值.
,無極大值.
綜上所述,單調遞增區間為![]() ;單調遞減區間為
;單調遞減區間為![]() ;
;![]() 極小值為2,無極大值;
極小值為2,無極大值;
(2)由![]() ,
,
則![]() ,
,
若![]() 有兩個極值點,則
有兩個極值點,則![]() 有兩個根
有兩個根
即![]() 有兩解,即
有兩解,即![]() ,
,
即![]() 與
與![]() 有兩個交點,
有兩個交點,
由(1)可知![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 上單調遞增,
上單調遞增,
![]() ,所以
,所以![]() ;
;
考慮函數 ,
,![]() ,
,
由洛必達法則: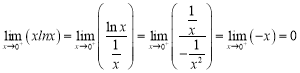 ,
,
![]() ,
,![]() ,
,
![]()
所以若![]() 與
與![]() 有兩個交點,則
有兩個交點,則![]() .
.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
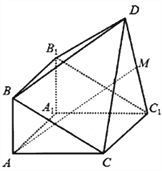
【題目】如圖,由直三棱柱![]() 和四棱錐
和四棱錐![]() 構成的幾何體中,
構成的幾何體中, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求證: ![]() ;
;
(Ⅱ)在線段![]() 上是否存在點
上是否存在點![]() ,使直線
,使直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ?若存在,求
?若存在,求![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在多邊形![]() 中,四邊形
中,四邊形![]() 為等腰梯形,
為等腰梯形,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() .以
.以![]() 為折痕把等腰梯形
為折痕把等腰梯形![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,如圖2所示.
,如圖2所示.


(1)證明:![]() 平面
平面![]() .
.
(2)求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新型冠狀病毒肺炎是一種急性感染性肺炎,其病原體是一種先前未在人類中發現的新型冠狀病毒,即2019新型冠狀病毒.2020年2月7日,國家衛健委決定將“新型冠狀病毒感染的肺炎”暫命名為“新型冠狀病毒肺炎”,簡稱“新冠肺炎”.患者初始癥狀多為發熱、乏力和干咳,并逐漸出現呼吸困難等嚴重表現.基于目前流行病學調查,潛伏期為1~14天,潛伏期具有傳染性,無癥狀感染者也可能成為傳染源.某市為了增強民眾防控病毒的意識,舉行了“預防新冠病毒知識競賽”網上答題,隨機抽取![]() 人,答題成績統計如圖所示.
人,答題成績統計如圖所示.
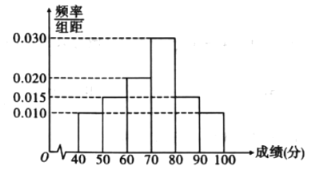
(1)由直方圖可認為答題者的成績![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 分別為答題者的平均成績
分別為答題者的平均成績![]() 和成績的方差
和成績的方差![]() ,那么這
,那么這![]() 名答題者成績超過
名答題者成績超過![]() 分的人數估計有多少人?(同一組中的數據用該組的區間中點值作代表)
分的人數估計有多少人?(同一組中的數據用該組的區間中點值作代表)
(2)如果成績超過![]() 分的民眾我們認為是“防御知識合格者”,用這
分的民眾我們認為是“防御知識合格者”,用這![]() 名答題者的成績來估計全市的民眾,現從全市中隨機抽取
名答題者的成績來估計全市的民眾,現從全市中隨機抽取![]() 人,“防御知識合格者”的人數為
人,“防御知識合格者”的人數為![]() ,求
,求![]() .(精確到
.(精確到![]() )
)
附:①![]() ,
,![]() ;②
;②![]() ,則
,則![]() ,
,![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,短軸的一個端點到右焦點的距離為2.
,短軸的一個端點到右焦點的距離為2.

(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 分別為橢圓
分別為橢圓![]() 的左、右頂點,如圖,過點
的左、右頂點,如圖,過點![]() 分別作直線
分別作直線![]() 與
與![]() ,設直線
,設直線![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() ,分別過
,分別過![]() 和
和![]() 作橢圓
作橢圓![]() 的兩條切線,且兩條切線交于點
的兩條切線,且兩條切線交于點![]() ,分別過
,分別過![]() 和
和![]() 作橢圓
作橢圓![]() 的兩條切線,且兩條切線交于點
的兩條切線,且兩條切線交于點![]() .證明:點
.證明:點![]() 在直線
在直線![]() 上.
上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】PM2.5是衡量空氣質量的重要指標,我國采用世衛組織的最寬值限定值,即PM2.5日均值在![]() 以下空氣質量為一級,在
以下空氣質量為一級,在![]() 空氣質量為二級,超過
空氣質量為二級,超過![]() 為超標,如圖是某地1月1日至10日的PM2.5(單位:
為超標,如圖是某地1月1日至10日的PM2.5(單位:![]() )的日均值,則下列說法正確的是( )
)的日均值,則下列說法正確的是( )

A.10天中PM2.5日均值最低的是1月3日
B.從1日到6日PM2.5日均值逐漸升高
C.這10天中恰有5天空氣質量不超標
D.這10天中PM2.5日均值的中位數是43
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以線段EF為直徑的圓內切于圓O:x2+y2=16.
(1)若點F的坐標為(﹣2,0),求點E的軌跡C的方程;
(2)在(1)的條件下,軌跡C上存在點T,使得![]() ,其中M,N為直線y=kx+b(b≠0)與軌跡C的交點,求△MNT的面積.
,其中M,N為直線y=kx+b(b≠0)與軌跡C的交點,求△MNT的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com