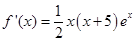已知函數 (
( ).
).
(1)當 時,求函數
時,求函數 的單調區間;
的單調區間;
(2)當 時,
時, 取得極值.
取得極值.
① 若 ,求函數
,求函數 在
在 上的最小值;
上的最小值;
② 求證:對任意 ,都有
,都有 .
.
(1)單調增區間為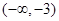 和
和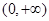 ,單調減區間為
,單調減區間為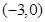 ;(2)①
;(2)①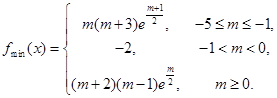 ②詳見解析.
②詳見解析.
解析試題分析:(1)求導解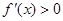 得
得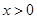 或
或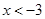 , 解
, 解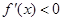 得
得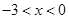 ;
;
(2)①當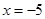 時,
時, 取得極值, 所以
取得極值, 所以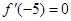 解得
解得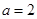 ,對
,對 求導,判斷在
求導,判斷在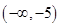 ,
,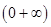 遞增,在
遞增,在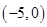 遞減,分類討論,求出最小值;②通過求導,求出
遞減,分類討論,求出最小值;②通過求導,求出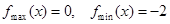 ,將恒成立問題轉化為最值問題,對任意
,將恒成立問題轉化為最值問題,對任意 ,都有
,都有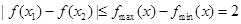 .
.
試題解析:(1)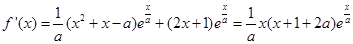
當 時,
時,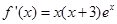
解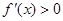 得
得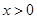 或
或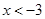 , 解
, 解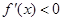 得
得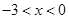
所以 單調增區間為
單調增區間為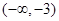 和
和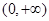 ,單調減區間為
,單調減區間為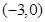
(2)①當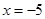 時,
時, 取得極值, 所以
取得極值, 所以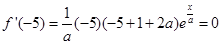
解得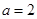 (經檢驗
(經檢驗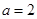 符合題意)
符合題意)