精英家教網> 2025年同步練習冊配套檢測卷九年級數學上冊魯教版五四制 > 第1頁 參考答案
2025年同步練習冊配套檢測卷九年級數學上冊魯教版五四制
注:目前有些書本章節名稱可能整理的還不是很完善,但都是按照順序排列的,請同學們按照順序仔細查找。練習冊2025年同步練習冊配套檢測卷九年級數學上冊魯教版五四制答案主要是用來給同學們做完題方便對答案用的,請勿直接抄襲。
1. 給出下列函數:①$y = 2x - 3$;②$y = \frac{1}{x}$;③$y = - 3x$。其中符合“當$x>0$時,函數值$y隨自變量的x$增大而減小”的是(
D
)
A.①③
B.③④
C.②④
D.②③
答案:D
解析:
① 對于函數 $y = 2x - 3$,它是一個一次函數,其斜率為 $2$,是一個正數,所以當 $x > 0$ 時,函數值 $y$ 隨 $x$ 的增大而增大,不符合題意。
② 對于函數 $y = \frac{1}{x}$,它是一個反比例函數。
根據反比例函數的性質,當 $x > 0$ 時,$y$ 隨 $x$ 的增大而減小,符合題意。
③ 對于函數 $y = -3x$,它是一個一次函數,其斜率為 $-3$,是一個負數,所以當 $x > 0$ 時,函數值 $y$ 隨 $x$ 的增大而減小,符合題意。
(題目中只給出了三個函數,沒有第四個函數,所以④不用考慮)
綜合以上分析,符合題意的有②和③。
2. 若點$A(x_{1}, - 6)$,$B(x_{2}, - 2)$,$C(x_{3},2)在反比例函數y = - \frac{4}{x}$的圖象上,則$x_{1}$,$x_{2}$,$x_{3}$的大小關系是(
B
)
A.$x_{1}<x_{2}<x_{3}$
B.$x_{3}<x_{1}<x_{2}$
C.$x_{2}<x_{3}<x_{1}$
D.$x_{2}<x_{1}<x_{3}$
答案:B
解析:
因為點$A(x_{1}, - 6)$,$B(x_{2}, - 2)$,$C(x_{3},2)$在反比例函數$y = -\frac{4}{x}$的圖象上,將各點的$y$坐標代入方程:
對于點$A$,$ -6 = -\frac{4}{x_{1}} \implies x_{1} = \frac{4}{6} = \frac{2}{3}$。
對于點$B$,$ -2 = -\frac{4}{x_{2}} \implies x_{2} = \frac{4}{2} = 2$。
對于點$C$,$2 = -\frac{4}{x_{3}} \implies x_{3} = -\frac{4}{2} = -2$。
比較$x_{1}$,$x_{2}$,$x_{3}$的大小,得到$x_{3} < x_{1} < x_{2}$。
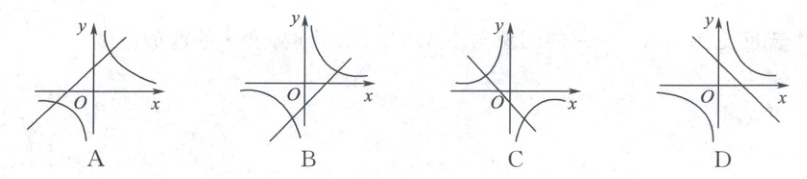
3. 在同一坐標系中,函數$y = \frac{k}{x}和y = - kx + 3$的大致圖象可能是(
D
)
答案:D
解析:
1. 一次函數$y = -kx + 3$與y軸交于點$(0, 3)$,故直線必過y軸正半軸,排除B、C;
2. 若直線$y = -kx + 3$為增函數(從左到右上升),則斜率$-k > 0$,即$k < 0$,此時反比例函數$y = \frac{k}{x}$圖象在第二、四象限,A中雙曲線在第一、三象限,矛盾,排除A;
3. 若直線為減函數(從左到右下降),則斜率$-k < 0$,即$k > 0$,此時反比例函數$y = \frac{k}{x}$圖象在第一、三象限,D符合.
4. 點$M(x_{1},y_{1})和點N(x_{2},y_{2})在反比例函數y = \frac{k^{2} - 2k + 3}{x}$($k$為常數)的圖象上。若$x_{1}<0<x_{2}$,則$y_{1}$,$y_{2}$,$0$的大小關系為(
C
)
A.$y_{1}<y_{2}<0$
B.$y_{1}>y_{2}>0$
C.$y_{1}<0<y_{2}$
D.$y_{1}>0>y_{2}$
答案:C
解析:
先化簡反比例函數的比例系數:$k^2 - 2k + 3 = (k - 1)^2 + 2$,因為$(k - 1)^2 \geq 0$,所以$(k - 1)^2 + 2 \geq 2 > 0$,即比例系數為正數。反比例函數$y = \frac{m}{x}$($m > 0$)的圖象在第一、三象限,在每個象限內$y$隨$x$的增大而減小。已知$x_1 < 0 < x_2$,則點$M$在第三象限,$y_1 < 0$;點$N$在第一象限,$y_2 > 0$,所以$y_1 < 0 < y_2$。
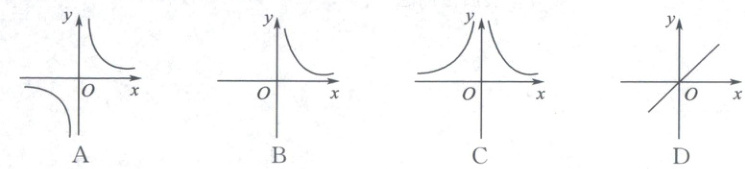
5. 如果矩形的面積為 8,那么它的長$y與寬x$的函數關系圖象大致表示為(
B
)
答案:B
解析:
由矩形的面積公式$S=xy$,已知面積為8,可得$xy=8$,變形得到$y=\frac{8}{x}$。
因為$x\gt0$,$y\gt0$,所以函數圖象只在第一象限。
該函數是反比例函數,其圖象是雙曲線。


