2025年全程助學與學習評估九年級數(shù)學上冊浙教版
注:目前有些書本章節(jié)名稱可能整理的還不是很完善,但都是按照順序排列的,請同學們按照順序仔細查找。練習冊2025年全程助學與學習評估九年級數(shù)學上冊浙教版答案主要是用來給同學們做完題方便對答案用的,請勿直接抄襲。
1. 下列函數(shù)中,不一定是二次函數(shù)的是(
D
)
A.$ y = 5x^{2} + 1 $
B.$ y = - 2x^{2} + 3x $
C.$ y = - 5x^{2} $
D.$ y = ax^{2} + bx + c $
答案:D
解析:
形如$y = ax^{2}+bx + c$($a\neq0$,$a$、$b$、$c$是常數(shù))的函數(shù)叫做二次函數(shù)。
選項A中$y = 5x^{2}+1$,其中$a = 5\neq0$,是二次函數(shù);
選項B中$y=-2x^{2}+3x$,其中$a=-2\neq0$,是二次函數(shù);
選項C中$y = - 5x^{2}$,其中$a=-5\neq0$,是二次函數(shù);
選項D中$y = ax^{2}+bx + c$,當$a = 0$時,函數(shù)變?yōu)?y=bx + c$,是一次函數(shù),不一定是二次函數(shù)。
2. 若二次函數(shù) $ y = ( - 2x + 1 ) ^{2} - 5 $ 的二次項系數(shù)為 $ a $,一次項系數(shù)為 $ b $,常數(shù)項為 $ c $,則 $ b^{2} - 4ac = $
80
.
答案:80
解析:
將二次函數(shù)$y=(-2x + 1)^2 - 5$展開:$\begin{aligned}y&=( -2x)^2 + 2×(-2x)×1 + 1^2 - 5\\&=4x^2 - 4x + 1 - 5\\&=4x^2 - 4x - 4\end{aligned}$可得$a=4$,$b=-4$,$c=-4$。則$b^2 - 4ac=(-4)^2 - 4×4×(-4)=16 + 64=80$。
3. 某工廠第一年的利潤為 30 萬元,第三年的利潤 $ y $(萬元)與平均年增長率 $ x $ 之間的函數(shù)表達式是
$y = 30(1 + x)^{2}$
.
答案:$y = 30(1 + x)^{2}$
解析:
設(shè)平均年增長率為$x$,第一年的利潤為30萬元,則第二年的利潤為$30(1 + x)$萬元,第三年的利潤相對于第二年繼續(xù)增長$x$,則第三年的利潤為$30(1 + x)(1 + x) = 30(1 + x)^{2}$萬元。
所以,第三年的利潤$y$(萬元)與平均年增長率$x$之間的函數(shù)表達式是$y = 30(1 + x)^{2}$,且由于增長率$x$應為正數(shù),所以$x$的取值范圍為$x>0$(或?qū)懗?x$為實數(shù)且$x > - 1$且$x\neq0$等合理形式均可,題目未要求可不寫出),該函數(shù)表達式已滿足題目要求。
4. 正方形的邊長為 3,若邊長增加 $ x $,那么面積增加 $ y $,則 $ y $ 與 $ x $ 之間的函數(shù)表達式是(
C
)
A.$ y = x^{2} + 9 $
B.$ y = ( x + 3 ) ^{2} $
C.$ y = x^{2} + 6x $
D.$ y = 9 - x^{2} $
答案:C
解析:
原正方形邊長為3,面積為 $3^2 = 9$。邊長增加 $x$ 后,新邊長為 $3 + x$,新面積為 $(3 + x)^2$。面積增加量為 $y = (3 + x)^2 - 9$,展開得 $y = 9 + 6x + x^2 - 9 = x^2 + 6x$。因此,$y$ 與 $x$ 的函數(shù)表達式為 $y = x^2 + 6x$。
5. 已知二次函數(shù) $ y = 2x^{2} + bx - c $,當 $ x = - 2 $ 時,$ y = 0 $;當 $ x = 3 $ 時,$ y = 0 $.
(1)求 $ b $,$ c $ 的值.
(2)當 $ x = - 3 $ 時,求 $ y $ 的值.
答案:(1)將$x=-2$,$y=0$代入$y=2x^{2}+bx - c$,得$2×(-2)^{2}+b×(-2)-c=0$,即$8 - 2b - c=0$;將$x=3$,$y=0$代入,得$2×3^{2}+b×3 - c=0$,即$18 + 3b - c=0$。聯(lián)立方程組$\begin{cases}8 - 2b - c=0\\18 + 3b - c=0\end{cases}$,兩式相減得$10 + 5b=0$,解得$b=-2$,代入$8 - 2×(-2)-c=0$,得$c=12$。
(2)由(1)知二次函數(shù)為$y=2x^{2}-2x - 12$,當$x=-3$時,$y=2×(-3)^{2}-2×(-3)-12=18 + 6 - 12=12$。
(1)$b=-2$,$c=12$;(2)$12$
6. 如圖,一塊矩形草地的長為 100m,寬為 80m,欲在中間修筑兩條互相垂直的寬為 $ x $(m)的小路,這時草坪的面積為 $ y $($ m^{2} $).求 $ y $ 與 $ x $ 的函數(shù)關(guān)系式,并求出 $ x $ 的取值范圍.
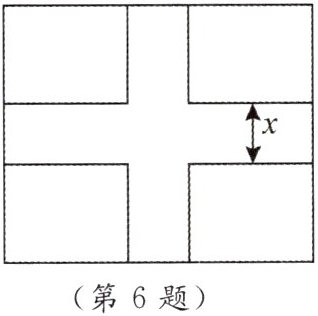
]
答案:由題意,兩條小路互相垂直,寬均為$x$m。
矩形草地的長為$100$m,修筑一條寬為$x$m的縱向小路后,剩余草坪的長為$(100 - x)$m;寬為$80$m,修筑一條寬為$x$m的橫向小路后,剩余草坪的寬為$(80 - x)$m。
草坪面積$y=(100 - x)(80 - x)$,展開得:
$y=100×80 - 100x - 80x + x2 = x2 - 180x + 8000$
因為小路寬$x$必須為正數(shù),且不能超過草地的長和寬,所以$x > 0$,$100 - x > 0$,$80 - x > 0$,即$0 < x < 80$。
綜上,$y$與$x$的函數(shù)關(guān)系式為$y = x2 - 180x + 8000$,$x$的取值范圍是$0 < x < 80$。

 ]
]