精英家教網> 2025年暑假生活八年級數學河北少年兒童出版社 > 第1頁 參考答案
2025年暑假生活八年級數學河北少年兒童出版社
注:目前有些書本章節名稱可能整理的還不是很完善,但都是按照順序排列的,請同學們按照順序仔細查找。練習冊2025年暑假生活八年級數學河北少年兒童出版社答案主要是用來給同學們做完題方便對答案用的,請勿直接抄襲。
1. 使式子$\sqrt {2x+1}$在實數范圍內有意義的x的取值范圍是
$x \geq -\frac{1}{2}$
.
答案:【解析】:
為了使$\sqrt{2x+1}$在實數范圍內有意義,被開方數$2x+1$必須是非負數。
因此,我們設置不等式:
$2x + 1 \geq 0$
解這個不等式,我們得到:
$2x \geq -1$
$x \geq -\frac{1}{2}$
【答案】:
$x \geq -\frac{1}{2}$
2. 在一次函數$y= (2-k)x+1$中,若$y隨x$的增大而增大,則$k$的取值范圍為______
$k<2$
.
答案:【解析】:對于一次函數$y = mx + b$($m$、$b$為常數,$m\neq0$),當$m>0$時,$y$隨$x$的增大而增大。在函數$y=(2 - k)x + 1$中,斜率$m = 2 - k$。因為$y$隨$x$的增大而增大,所以$2 - k>0$,解這個不等式可得$k<2$。
【答案】:$k<2$
3. 在一個四邊形中,最多能有
3
個銳角,最多能有
3
個鈍角.
答案:【解析】:對于四邊形中銳角的個數,因為銳角是小于$90^{\circ}$的角,假設四邊形有$4$個銳角,那么四個內角之和會小于$4×90^{\circ}=360^{\circ}$,這與四邊形內角和是$360^{\circ}$矛盾;若有$3$個銳角,設這$3$個銳角都接近$90^{\circ}$,比如都為$89^{\circ}$,則第四個角為$360^{\circ}-3×89^{\circ}=360^{\circ}-267^{\circ}=93^{\circ}$,是合理的,所以最多有$3$個銳角。
對于鈍角的個數,鈍角是大于$90^{\circ}$小于$180^{\circ}$的角,假設四邊形有$4$個鈍角,那么四個內角之和會大于$4×90^{\circ}=360^{\circ}$且小于$4×180^{\circ}=720^{\circ}$,但四邊形內角和固定為$360^{\circ}$,$4$個鈍角之和必然大于$360^{\circ}$,矛盾;若有$3$個鈍角,設這$3$個鈍角都接近$180^{\circ}$,比如都為$91^{\circ}$,則第四個角為$360^{\circ}-3×91^{\circ}=360^{\circ}-273^{\circ}=87^{\circ}$,是合理的,所以最多有$3$個鈍角。
【答案】:3,3
4. 某班圍繞“舞蹈、樂器、聲樂、其他項目中,你最喜歡哪項活動(每人只限選一項)”的問題,對全班50名學生進行問卷調查,調查結果如圖1-1所示的扇形統計圖,則該班喜歡樂器的學生有
22
名.
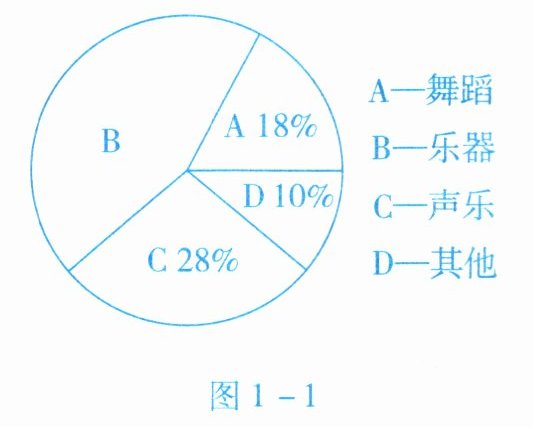
答案:【解析】:根據扇形統計圖可知,喜歡樂器的學生所占比例為:
$1 - 18\% - 28\% - 10\% = 44\%$。
該班學生總人數為$50$名,所以喜歡樂器的學生人數為:
$50× 44\% = 50×0.44 = 22$(名)。
【答案】:$22$
5. 如圖$1-2$所示,在矩形$ABCD$中,對角線$AC$,$BD相交于點O$,點$E$,$F分別是AO$,$AD$的中點. 若$AB= 6cm$,$BC= 8cm$,則$\triangle AEF$的周長為______
9
$cm$.
答案:【解析】:
首先,由于$ABCD$是矩形,所以根據勾股定理,有$AC = \sqrt{AB^2 + BC^2} = \sqrt{6^2 + 8^2} = 10 \text{ cm}$。
由于$O$是對角線$AC$和$BD$的交點,根據矩形的性質,$O$是$AC$的中點,所以$AO = \frac{AC}{2} = 5 \text{ cm}$。
點$E$是$AO$的中點,所以$AE = \frac{AO}{2} = 2.5 \text{ cm}$。
點$F$是$AD$的中點,由于$AD = BC = 8 \text{ cm}$,所以$AF = \frac{AD}{2} = 4 \text{ cm}$。
由于$E$和$F$分別是$AO$和$AD$的中點,根據中位線的性質,$EF$是$\triangle AOD$的中位線,所以$EF = \frac{1}{2}OD = \frac{1}{2} × \frac{1}{2}BD = \frac{1}{4}AC = 2.5 \text{ cm}$(這里用到了$OD = \frac{1}{2}BD$和$BD = AC$)。
最后,$\triangle AEF$的周長為$AE + AF + EF = 2.5 + 4 + 2.5 = 9 \text{ cm}$。
【答案】:9
1. 矩形的兩條對角線的夾角是$120^{\circ }$,較短的邊長是$4cm$,則其較長的邊長是(
C
)
A.$8\sqrt {3}cm$
B.$8cm$
C.$4\sqrt {3}cm$
D.$4cm$
答案:【解析】:在矩形中,對角線相等且互相平分,所以兩條對角線與矩形兩邊構成的三角形中,兩條對角線的一半相等。已知兩條對角線的夾角是$120^{\circ}$,則其鄰補角為$60^{\circ}$。較短的邊長與兩條對角線的一半構成一個等邊三角形(因為夾角為$60^{\circ}$且兩邊相等),所以對角線的一半等于較短邊長$4cm$,則對角線長為$8cm$。
設較長的邊長為$x cm$,根據勾股定理,較短邊、較長邊與對角線構成直角三角形,可得:$4^{2} + x^{2} = 8^{2}$,即$16 + x^{2} = 64$,解得$x^{2} = 48$,$x = 4\sqrt{3}$(負值舍去)。
【答案】:C
2. 下列計算錯誤的是(
B
)
A.$\sqrt {2}\cdot \sqrt {3}= \sqrt {6}$
B.$\sqrt {2}+\sqrt {3}= \sqrt {6}$
C.$\sqrt {12}÷ \sqrt {3}= 2$
D.$\sqrt {8}= 2\sqrt {2}$
答案:【解析】:逐一分析各選項:
選項A:根據二次根式乘法法則,$\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}$($a\geq0$,$b\geq0$),所以$\sqrt{2} \cdot \sqrt{3} = \sqrt{2×3} = \sqrt{6}$,計算正確。
選項B:$\sqrt{2}$和$\sqrt{3}$不是同類二次根式,不能直接合并,$\sqrt{2} + \sqrt{3}$已是最簡形式,不能等于$\sqrt{6}$,計算錯誤。
選項C:根據二次根式除法法則,$\sqrt{a} ÷ \sqrt{b} = \sqrt{\frac{a}{b}}$($a\geq0$,$b>0$),所以$\sqrt{12} ÷ \sqrt{3} = \sqrt{\frac{12}{3}} = \sqrt{4} = 2$,計算正確。
選項D:$\sqrt{8} = \sqrt{4×2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2}$,計算正確。
綜上,計算錯誤的是選項B。
【答案】:B

